Near to Far Field Spectra#
The near-to-far field transformation feature in Cartesian (2D/3D) and cylindrical coordinates is demonstrated using six different examples. Generally, there are three steps involved in this type of calculation. First, the "near" surface(s) is defined as a set of surfaces capturing all outgoing radiation in free space in the desired direction(s). Second, the simulation is run using a pulsed source (or alternatively, a CW source via the frequency-domain solver) to allow Meep to accumulate the DFT fields on the near surface(s). Third, Meep computes the "far" fields at any desired points with the option to save the far fields to an HDF5 file.
Radiation Pattern of an Antenna#
In this example, we compute the radiation pattern of an antenna in free space. The calculation involves computing the far fields of an electric-current point dipole emitter in vacuum. The source is placed at the center of a 2D cell surrounded by PML. The near fields are obtained on a bounding box defined along the edges of the non-PML region. The far fields are computed in two ways from closed surfaces: (1) sides of a square and (2) circumference of a circle, having a length or radius many times larger than the source wavelength and lying beyond the cell. From both the near and far fields, we will also compute the total outgoing Poynting flux and demonstrate that they are equivalent. Results will be shown for three orthogonal dipole orientations and verified using antenna theory.
The simulation geometry is shown in the following schematic.

In the first part of the simulation, we define the cell and source as well as the near field and flux regions. Since we are using a pulsed source (with center wavelength of 1 μm), the fields are timestepped until they have sufficiently decayed away.
The simulation script is in examples/antenna-radiation.py. The notebook is examples/antenna-radiation.ipynb.
import meep as mp
import math
import numpy as np
import matplotlib.pyplot as plt
resolution = 50 # pixels/um
sxy = 4
dpml = 1
cell = mp.Vector3(sxy+2*dpml,sxy+2*dpml)
pml_layers = [mp.PML(dpml)]
fcen = 1.0
df = 0.4
src_cmpt = mp.Ex
sources = [mp.Source(src=mp.GaussianSource(fcen,fwidth=df),
center=mp.Vector3(),
component=src_cmpt)]
if src_cmpt == mp.Ex:
symmetries = [mp.Mirror(mp.X,phase=-1),
mp.Mirror(mp.Y,phase=+1)]
elif src_cmpt == mp.Ey:
symmetries = [mp.Mirror(mp.X,phase=+1),
mp.Mirror(mp.Y,phase=-1)]
elif src_cmpt == mp.Ez:
symmetries = [mp.Mirror(mp.X,phase=+1),
mp.Mirror(mp.Y,phase=+1)]
else:
symmetries = []
sim = mp.Simulation(cell_size=cell,
resolution=resolution,
sources=sources,
symmetries=symmetries,
boundary_layers=pml_layers)
nearfield_box = sim.add_near2far(fcen, 0, 1,
mp.Near2FarRegion(center=mp.Vector3(0,+0.5*sxy),
size=mp.Vector3(sxy,0)),
mp.Near2FarRegion(center=mp.Vector3(0,-0.5*sxy),
size=mp.Vector3(sxy,0),
weight=-1),
mp.Near2FarRegion(center=mp.Vector3(+0.5*sxy,0),
size=mp.Vector3(0,sxy)),
mp.Near2FarRegion(center=mp.Vector3(-0.5*sxy,0),
size=mp.Vector3(0,sxy),
weight=-1))
flux_box = sim.add_flux(fcen, 0, 1,
mp.FluxRegion(center=mp.Vector3(0,+0.5*sxy),
size=mp.Vector3(sxy,0)),
mp.FluxRegion(center=mp.Vector3(0,-0.5*sxy),
size=mp.Vector3(sxy,0),
weight=-1),
mp.FluxRegion(center=mp.Vector3(+0.5*sxy,0),
size=mp.Vector3(0,sxy)),
mp.FluxRegion(center=mp.Vector3(-0.5*sxy,0),
size=mp.Vector3(0,sxy),
weight=-1))
sim.run(until_after_sources=mp.stop_when_dft_decayed())
After the time stepping, the flux of the near fields is computed using get_fluxes:
near_flux = mp.get_fluxes(flux_box)[0]
In the first of two cases, the flux of the far fields is computed using the flux routine for a square box of side length 2 mm which is 2000 times larger than the source wavelength. This requires computing the outgoing flux on each of the four sides of the box separately and summing the values. The resolution of the far fields is chosen arbitrarily as 1 point/μm. This means there are 2x106 points per side length.
# half side length of far-field square box OR radius of far-field circle
r = 1000/fcen
# resolution of far fields (points/μm)
res_ff = 1
far_flux_box = (nearfield_box.flux(mp.Y,
mp.Volume(center=mp.Vector3(y=r),
size=mp.Vector3(2*r)),
res_ff)[0] -
nearfield_box.flux(mp.Y,
mp.Volume(center=mp.Vector3(y=-r),
size=mp.Vector3(2*r)),
res_ff)[0] +
nearfield_box.flux(mp.X,
mp.Volume(center=mp.Vector3(r),
size=mp.Vector3(y=2*r)),
res_ff)[0] -
nearfield_box.flux(mp.X,
mp.Volume(center=mp.Vector3(-r),
size=mp.Vector3(y=2*r)),
res_ff)[0])
For the second of two cases, we use the get_farfield routine to compute the far fields by looping over a set of 100 equally spaced points along the circumference of a circle with radius of 1 mm. The six far field components (, , , , , ) are stored as separate arrays of complex numbers. From the far fields at each point , we compute the outgoing or radial flux: , where and are the components of the Poynting vector . Note that is always 0 since this is a 2D simulation. The total flux is computed and the three flux values are displayed.
npts = 100 # number of points in [0,2*pi) range of angles
angles = 2*math.pi/npts*np.arange(npts)
E = np.zeros((npts,3),dtype=np.complex128)
H = np.zeros((npts,3),dtype=np.complex128)
for n in range(npts):
ff = sim.get_farfield(nearfield_box,
mp.Vector3(r*math.cos(angles[n]),
r*math.sin(angles[n])))
E[n,:] = [ff[j] for j in range(3)]
H[n,:] = [ff[j+3] for j in range(3)]
Px = np.real(np.conj(E[:, 1]) * H[:, 2] - np.conj(E[:, 2]) * H[:, 1])
Py = np.real(np.conj(E[:, 2]) * H[:, 0] - np.conj(E[:, 0]) * H[:, 2])
Pr = np.sqrt(np.square(Px) + np.square(Py))
# integrate the radial flux over the circle circumference
far_flux_circle = np.sum(Pr)*2*np.pi*r/len(Pr)
print("flux:, {:.6f}, {:.6f}, {:.6f}".format(near_flux,far_flux_box,far_flux_circle))
# Analytic formulas for the radiation pattern as the Poynting vector
# of an electric dipole in vacuum. From Section 4.2 "Infinitesimal Dipole"
# of Antenna Theory: Analysis and Design, 4th Edition (2016) by C. Balanis.
if src_cmpt == mp.Ex:
flux_theory = np.sin(angles) ** 2
elif src_cmpt == mp.Ey:
flux_theory = np.cos(angles) ** 2
elif src_cmpt == mp.Ez:
flux_theory = np.ones((npts,))
fig, ax = plt.subplots(subplot_kw={"projection": "polar"}, figsize=(6, 6))
ax.plot(angles,Pr/max(Pr),'b-')
ax.set_rmax(1)
ax.set_rticks([0,0.5,1])
ax.grid(True)
ax.set_rlabel_position(22)
ax.legend()
if mp.am_master():
fig.savefig(
f"radiation_pattern_{mp.component_name(src_cmpt)}.png",
dpi=150,
bbox_inches="tight",
)
By Poynting's theorem, the total outgoing flux obtained by integrating around a closed surface should be the same whether it is calculated from the near or far fields (unless there are sources or absorbers in between). The flux of the near fields for the source is 2.456196 and that for the far fields is 2.458030 (box) and 2.457249 (circle). The ratio of near- to far-field (circle) flux is 0.999571. Similarly, for the source, the values are 1.227786 (near-field), 1.227651 (far-field box), and 1.227260 (far-field circle). The ratio of near- to far-field (circle) flux is 1.000429. The slight differences in the flux values are due to discretization effects and will decrease as the resolution is increased.
From antenna theory, a linearly polarized dipole with orientation along produces a radiation pattern in 2D. This contains two lobes (a "dipole") at and . The same radiation pattern in 3D resembles a "donut." For reference, see Section 4.2 "Infinitesimal Dipole" of Antenna Theory: Analysis and Design, 4th Edition (2016) by C Balanis.
Finally, we plot the radial flux normalized by its maximum value over the entire interval to obtain a range of values between 0 and 1. These are shown below in the linearly scaled, polar-coordinate plots. The three figures are obtained using separate runs involving a src_cmpt of , , and . As expected, the and sources produce dipole radiation patterns while has a monopole pattern. The radiation pattern from the simulation agrees with the analytic result for all three dipole orientations.
ax = plt.subplot(111, projection='polar')
ax.plot(angles,Pr/max(Pr),'b-')
ax.set_rmax(1)
ax.set_rticks([0,0.5,1])
ax.grid(True)
ax.set_rlabel_position(22)
plt.show()

Antenna above a Perfect Electric Conductor Ground Plane#
As a second example, we compute the radiation pattern of an antenna positioned a given height above a perfect-electric conductor (PEC) ground plane. Depending on the wavelength and height of the antenna, self-interference effects due to reflections from the ground plane will produce well-defined lobes in the radiation pattern. The challenge in setting up this calculation is that because the ground plane is infinitely extended, it is not possible to enclose the antenna by a near-field surface. A non-closed near-field surface unfortunately gives rise to truncation errors which is described in more detail in the section below.
A workaround is to transform this problem into radiation in free space by making use of the fact that the effect of the ground plane can be exactly reproduced by two antennas of opposite phase separated by a distance of . This is known as the method of images. Additionally, the odd-mirror symmetry plane can be used to divide the cell in half in order to reduce the computational cost.
We can validate the radiation pattern computed by Meep using analytic theory. The radiation pattern of a two-element antenna array is equivalent to the radiation pattern of a single antenna multiplied by its "array factor" (AF) as derived in Section 6.2 "Two-Element Array" of Antenna Theory: Analysis and Design, Fourth Edition (2016) by C.A. Balanis. In this example, we consider an -polarized antenna at a vacuum wavelength () of 0.65 μm embedded within a medium with of 1.2 and positioned 1.25 μm above the ground plane. The outgoing (radial) flux is computed along the circumference of a circle with radius 1000 (or 650 μm) centered at the midpoint between the two antennas. The angular range is [0,90] degrees with 0° being the direction normal to the ground plane. A schematic showing the simulation layout and a plot of the radiation pattern computed by Meep and analytic theory are shown in the figure below. There is good agreement between the two results.
The simulation script is in examples/antenna_pec_ground_plane.py.

resolution = 200 # pixels/um
n = 1.2 # refractive index of surrounding medium
h = 1.25 # height of antenna (point dipole source) above ground plane
wvl = 0.65 # vacuum wavelength
r = 1000*wvl # radius of far-field circle
npts = 50 # number of points in [0,pi/2) range of angles
angles = 0.5*math.pi/npts*np.arange(npts)
def radial_flux(sim,nearfield_box,r):
E = np.zeros((npts,3),dtype=np.complex128)
H = np.zeros((npts,3),dtype=np.complex128)
for n in range(npts):
ff = sim.get_farfield(nearfield_box,
mp.Vector3(r*math.sin(angles[n]),
r*math.cos(angles[n])))
E[n,:] = [np.conj(ff[j]) for j in range(3)]
H[n,:] = [ff[j+3] for j in range(3)]
Px = np.real(E[:,1]*H[:,2]-E[:,2]*H[:,1]) # Ey*Hz-Ez*Hy
Py = np.real(E[:,2]*H[:,0]-E[:,0]*H[:,2]) # Ez*Hx-Ex*Hz
Pr = np.sqrt(np.square(Px)+np.square(Py))
return Pr
def free_space_radiation(src_cmpt):
sxy = 4
dpml = 1
cell_size = mp.Vector3(sxy+2*dpml,sxy+2*dpml)
pml_layers = [mp.PML(dpml)]
fcen = 1/wvl
sources = [mp.Source(src=mp.GaussianSource(fcen,fwidth=0.2*fcen),
center=mp.Vector3(),
component=src_cmpt)]
if src_cmpt == mp.Hz:
symmetries = [mp.Mirror(mp.X,phase=-1),
mp.Mirror(mp.Y,phase=-1)]
elif src_cmpt == mp.Ez:
symmetries = [mp.Mirror(mp.X,phase=+1),
mp.Mirror(mp.Y,phase=+1)]
else:
symmetries = []
sim = mp.Simulation(cell_size=cell_size,
resolution=resolution,
sources=sources,
symmetries=symmetries,
boundary_layers=pml_layers,
default_material=mp.Medium(index=n))
nearfield_box = sim.add_near2far(fcen,
0,
1,
mp.Near2FarRegion(center=mp.Vector3(0,+0.5*sxy),
size=mp.Vector3(sxy,0)),
mp.Near2FarRegion(center=mp.Vector3(0,-0.5*sxy),
size=mp.Vector3(sxy,0),
weight=-1),
mp.Near2FarRegion(center=mp.Vector3(+0.5*sxy,0),
size=mp.Vector3(0,sxy)),
mp.Near2FarRegion(center=mp.Vector3(-0.5*sxy,0),
size=mp.Vector3(0,sxy),
weight=-1))
sim.run(until_after_sources=mp.stop_when_dft_decayed())
Pr = radial_flux(sim,nearfield_box,r)
return Pr
def pec_ground_plane_radiation(src_cmpt=mp.Hz):
L = 8.0 # length of non-PML region
dpml = 1.0 # thickness of PML
sxy = dpml+L+dpml
cell_size = mp.Vector3(sxy,sxy,0)
boundary_layers = [mp.PML(dpml)]
fcen = 1/wvl
# The near-to-far field transformation feature only supports
# homogeneous media which means it cannot explicitly take into
# account the ground plane. As a workaround, we use two antennas
# of opposite sign surrounded by a single near2far box which
# encloses both antennas. We then use an odd mirror symmetry to
# divide the computational cell in half which is effectively
# equivalent to a PEC boundary condition on one side.
# Note: This setup means that the radiation pattern can only
# be measured in the top half above the dipole.
sources = [mp.Source(src=mp.GaussianSource(fcen,fwidth=0.2*fcen),
component=src_cmpt,
center=mp.Vector3(0,+h)),
mp.Source(src=mp.GaussianSource(fcen,fwidth=0.2*fcen),
component=src_cmpt,
center=mp.Vector3(0,-h),
amplitude=-1 if src_cmpt==mp.Ez else +1)]
symmetries = [mp.Mirror(direction=mp.X,
phase=+1 if src_cmpt==mp.Ez else -1),
mp.Mirror(direction=mp.Y,
phase=-1 if src_cmpt==mp.Ez else +1)]
sim = mp.Simulation(resolution=resolution,
cell_size=cell_size,
boundary_layers=boundary_layers,
sources=sources,
symmetries=symmetries,
default_material=mp.Medium(index=n))
nearfield_box = sim.add_near2far(fcen,
0,
1,
mp.Near2FarRegion(center=mp.Vector3(0,2*h),
size=mp.Vector3(2*h,0),
weight=+1),
mp.Near2FarRegion(center=mp.Vector3(0,-2*h),
size=mp.Vector3(2*h,0),
weight=-1),
mp.Near2FarRegion(center=mp.Vector3(h,0),
size=mp.Vector3(0,4*h),
weight=+1),
mp.Near2FarRegion(center=mp.Vector3(-h,0),
size=mp.Vector3(0,4*h),
weight=-1))
sim.plot2D()
plt.savefig('antenna_pec_ground_plane.png',bbox_inches='tight')
sim.run(until_after_sources=mp.stop_when_dft_decayed())
Pr = radial_flux(sim,nearfield_box,r)
return Pr
if __name__ == '__main__':
src_cmpt = mp.Ez # TM/P: Hz or TE/S: Ez
Pr_fsp = free_space_radiation(src_cmpt)
Pr_pec = pec_ground_plane_radiation(src_cmpt)
# The radiation pattern of a two-element antenna
# array is equivalent to the radiation pattern of
# a single antenna multiplied by its array factor
# as derived in Section 6.2 "Two-Element Array" of
# Antenna Theory: Analysis and Design, Fourth Edition
# (2016) by C.A. Balanis.
k = 2*np.pi/(wvl/n) # wavevector in free space
Pr_theory = np.zeros(npts,)
for i,ang in enumerate(angles):
Pr_theory[i] = Pr_fsp[i] * 2*np.sin(k*h*np.cos(ang))
Pr_pec_norm = Pr_pec/np.max(Pr_pec)
Pr_theory_norm = (Pr_theory/max(Pr_theory))**2
plt.figure()
plt.plot(np.degrees(angles),Pr_pec_norm,'b-',label='Meep')
plt.plot(np.degrees(angles),Pr_theory_norm,'r-',label='theory')
plt.xlabel('angle (degrees)')
plt.ylabel('radial flux (normalized by maximum flux)')
plt.title('antenna with {}$_z$ polarization above PEC ground plane'.format('E' if src_cmpt==mp.Ez else r'H'))
plt.axis([0,90,0,1.0])
plt.legend()
plt.savefig('radiation_pattern.png',bbox_inches='tight')
print("norm:, {:.6f}".format(np.linalg.norm(Pr_pec_norm-Pr_theory_norm)))
Radiation Pattern of a Disc in Cylindrical Coordinates#
The near-to-far field transformation feature can also be used in cylindrical coordinates. As a demonstration, we compute the radiation pattern of a dielectric disc and verify Poynting's theorem: the total radiated flux computed from the far fields is equivalent to using the near fields via add_flux. (The same result is demonstrated in Tutorial/Radiation Pattern of an Antenna for 2D Cartesian coordinates.)
The simulation consists of an point-dipole source ( = 1.0 μm) at = 0.6 μm embedded within a disc (radius of 1.2 μm) of index = 2.4 above a perfect-metallic ground plane. This is similar to the configuration in Tutorial/Extraction Efficiency of a Light-Emitting Diode (LED). Unlike the infinitely extended slab of the LED, a finite structure such as the disc ensures that all the power from the dipole emitter is radiated. The LED contains waveguide modes which are more challenging to disentagle from the radiated power.
A schematic of the simulation layout is shown below. The flux and near-field monitors (shown in blue) are overlapping.

Obtaining the radiation pattern of the disc involves computing the radial (or "outgoing") flux from the far fields along the circumference of a quarter circle (i.e. angular range of ). The radius of the circle needs to be sufficiently large () to ensure accurate results but is otherwise arbitrary. The total flux is then computed by integrating over the surface of a hemisphere with radius in spherical coordinates:
An angular grid of equally spaced points in has . Note that the same weighting is necessary for the power in any cone, not just over all angles.
A plot of the radiation pattern in polar coordinates and 3D is shown below. Note regarding the coordinate axes in the polar plot: 0° is in the direction which is normal to the ground plane and 90° is in the direction which is parallel to the ground plane. This is consistent with the convention for the polar angle used in spherical coordinates. Also note that the radial flux is a dimensionful quantity but because Meep uses , , and its units are arbitrary.

The total flux computed using the near and far fields is shown to be in close agreement with a relative error of ~7%.
total_flux:, 643.65058 (near), 597.72713 (far), 0.07135 (error)
The error decreases with increasing (1) grid resolution, (2) runtime, and (3) number of angular grid points. However, this only applies to a closed near-field surface which is not the case in this example. This is because the ground plane, which extends to infinity, contains and fields on its surface which are not zero (unlike the and fields). These magnetic fields produce equivalent currents which radiate into the far field. The PML in the direction does not mitigate this effect.
Because the near-field surface actually extends to infinity in the direction, one approach to reducing the error introduced by its finite truncation would be to simply make the cell size in the direction larger (the parameter L in the script below). Another option which would remove this error entirely would be to simulate the same structure using a closed surface by removing the ground plane and duplicating the structure and source below the plane. This is known as the method of images. See Tutorial/Antenna above a Perfect Electric Conductor Ground Plane for a demonstration of this approach.
The simulation script is in examples/disc_radiation_pattern.py.
import math
from typing import Tuple
import matplotlib
import meep as mp
import numpy as np
matplotlib.use("agg")
import matplotlib.pyplot as plt
resolution = 100 # pixels/μm
dpml = 0.5 # thickness of PML
dair = 1.0 # thickness of air padding
L = 6.0 # length of non-PML region
n = 2.4 # refractive index of surrounding medium
wvl = 1.0 # wavelength (in vacuum)
fcen = 1 / wvl # center frequency of source/monitor
# field decay threshold for runtime termination criteria
tol = 1e-8
# number of angular grid points in [0, π/2]
npts = 100
# grid of polar angles for computing radiated flux in far field
thetas = np.linspace(0, 0.5 * math.pi, npts)
# radius of quarter circle for computing flux in far field
r = 1000 * wvl
def plot_radiation_pattern_polar(Ptheta: np.ndarray):
"""Plots the radiation pattern in polar coordinates.
The angles increase clockwise with zero at the top (+z direction).
Args:
Ptheta: radial flux of the far fields in polar coordinates.
"""
fig, ax = plt.subplots(subplot_kw={"projection": "polar"}, figsize=(6,6))
ax.plot(
thetas,
Ptheta,
"b-",
)
ax.set_theta_direction(-1)
ax.set_theta_offset(0.5 * math.pi)
ax.set_thetalim(0, 0.5 * math.pi)
ax.grid(True)
ax.set_rlabel_position(22)
ax.set_ylabel("radial flux (a.u.)")
ax.set_title("radiation pattern in polar coordinates")
if mp.am_master():
fig.savefig(
"led_radpattern_polar.png",
dpi=150,
bbox_inches="tight",
)
def plot_radiation_pattern_3d(Ptheta: np.ndarray):
"""Plots the radiation pattern in 3d Cartesian coordinates.
Args:
Ptheta: radial flux of the far fields in polar coordinates.
"""
phis = np.linspace(0, 2 * np.pi, npts)
xs = np.zeros((len(thetas), len(phis)))
ys = np.zeros((len(thetas), len(phis)))
zs = np.zeros((len(thetas), len(phis)))
for i, theta in enumerate(thetas):
for j, phi in enumerate(phis):
xs[i, j] = Ptheta[i] * np.sin(theta) * np.cos(phi)
ys[i, j] = Ptheta[i] * np.sin(theta) * np.sin(phi)
zs[i, j] = Ptheta[i] * np.cos(theta)
fig, ax = plt.subplots(subplot_kw={"projection": "3d"}, figsize=(6,6))
ax.plot_surface(xs, ys, zs, cmap="inferno")
ax.set_title("radiation pattern in 3d")
ax.set_box_aspect((np.amax(xs), np.amax(ys), np.amax(zs)))
ax.set_zlabel("radial flux (a.u.)")
ax.set(xticklabels=[], yticklabels=[])
if mp.am_master():
fig.savefig(
"led_radpattern_3d.png",
dpi=150,
bbox_inches="tight",
)
def radiation_pattern(sim: mp.Simulation, n2f_mon: mp.DftNear2Far) -> np.ndarray:
"""Computes the radiation pattern from the far fields.
Args:
sim: a `Simulation` object.
n2f_mon: a `DftNear2Far` object returned by `Simulation.add_near2far`.
Returns:
Array of radial Poynting flux, one for each point on the circumference of
a quarter circle with angular range of [0, π/2] rad. 0 rad is the +z
direction and π/2 is +r.
"""
E = np.zeros((npts, 3), dtype=np.complex128)
H = np.zeros((npts, 3), dtype=np.complex128)
for n in range(npts):
ff = sim.get_farfield(
n2f_mon, mp.Vector3(r * math.sin(thetas[n]), 0, r * math.cos(thetas[n]))
)
E[n, :] = [np.conj(ff[j]) for j in range(3)]
H[n, :] = [ff[j + 3] for j in range(3)]
Pr = np.real(E[:, 1] * H[:, 2] - E[:, 2] * H[:, 1])
Pz = np.real(E[:, 0] * H[:, 1] - E[:, 1] * H[:, 0])
Prz = np.sqrt(np.square(Pr) + np.square(Pz))
return Prz
def disc_total_flux(dmat: float, h: float) -> Tuple[float, float]:
"""Computes the total radiated flux from a point dipole embedded
within a dielectric disc above a lossless ground plane using
its near and far fields as separate calculations.
Args:
dmat: thickness of dielectric disc.
h: height of dipole above ground plane as fraction of dmat.
Returns:
A 2-tuple of the total flux computed using the near and far fields,
respectively.
"""
sr = L + dpml
sz = dmat + dair + dpml
cell_size = mp.Vector3(sr, 0, sz)
boundary_layers = [
mp.PML(dpml, direction=mp.R),
mp.PML(dpml, direction=mp.Z, side=mp.High),
]
src_cmpt = mp.Er
src_pt = mp.Vector3(0.1 * L, 0, -0.5 * sz + h * dmat)
sources = [
mp.Source(
src=mp.GaussianSource(fcen, fwidth=0.1 * fcen),
component=src_cmpt,
center=src_pt,
)
]
geometry = [
mp.Block(
material=mp.Medium(index=n),
center=mp.Vector3(0.1 * L, 0, -0.5 * sz + 0.5 * dmat),
size=mp.Vector3(0.2 * L, mp.inf, dmat),
)
]
sim = mp.Simulation(
resolution=resolution,
cell_size=cell_size,
dimensions=mp.CYLINDRICAL,
m=-1,
boundary_layers=boundary_layers,
sources=sources,
geometry=geometry,
)
# flux monitor
flux_mon = sim.add_flux(
fcen,
0,
1,
mp.FluxRegion(
center=mp.Vector3(0.5 * L, 0, 0.5 * sz - dpml),
size=mp.Vector3(L, 0, 0),
),
mp.FluxRegion(
center=mp.Vector3(L, 0, 0.5 * sz - dpml - 0.5 * (dair + dmat)),
size=mp.Vector3(0, 0, dair + dmat),
),
)
# near-field monitor
n2f_mon = sim.add_near2far(
fcen,
0,
1,
mp.FluxRegion(
center=mp.Vector3(0.5 * L, 0, 0.5 * sz - dpml),
size=mp.Vector3(L, 0, 0),
),
mp.FluxRegion(
center=mp.Vector3(L, 0, 0.5 * sz - dpml - 0.5 * (dair + dmat)),
size=mp.Vector3(0, 0, dair + dmat),
),
)
fig, ax = plt.subplots()
sim.plot2D(ax=ax)
if mp.am_master():
fig.savefig("disc_simulation_layout.png", dpi=150, bbox_inches="tight")
sim.run(
until_after_sources=mp.stop_when_fields_decayed(
50,
src_cmpt,
src_pt,
tol,
),
)
flux_near = mp.get_fluxes(flux_mon)[0]
Ptheta = radiation_pattern(sim, n2f_mon)
plot_radiation_pattern_polar(r * r * Ptheta)
plot_radiation_pattern_3d(r * r * Ptheta)
dtheta = 0.5 * math.pi / (npts - 1)
dphi = 2 * math.pi
flux_far = np.sum(Ptheta * np.sin(thetas)) * r * r * dtheta * dphi
return flux_near, flux_far
if __name__ == "__main__":
disc_thickness = 0.7 * wvl / n
dipole_height = 0.5
near_flux, far_flux = disc_total_flux(disc_thickness, dipole_height)
err = abs(near_flux - far_flux) / near_flux
print(
f"total_flux:, {near_flux:.5f} (near), {far_flux:.5f} (far), "
f"{err:.5f} (error)"
)
Extraction Efficiency of a Collection of Dipoles in a Disc#
Tutorial/Radiation Pattern of a Disc in Cylindrical Coordinates demonstrated the procedure for computing the radiation pattern of a single dipole (actually a "ring" current source with angular dependence ). Tutorial/Nonaxisymmetric Dipole Sources described the method for modeling a point dipole at in cylindrical coordinates using a Fourier-series expansion of the fields in . Tutorial/Extraction Efficiency of a Light-Emitting Diode described the procedure for computing the extraction efficiency of a dipole at . These three demonstrations can be combined to compute the extraction efficiency for a point dipole anywhere in the cylindrical cell. Computing the extraction efficiency of an actual light-emitting diode (LED), however, involves a collection of spatially incoherent dipole emitters. Tutorial/Stochastic Dipole Emission in Light Emitting Diodes described a method for computing the emission of a collection of dipoles using a series of single-dipole calculations and then averaging the emission profiles in post processing. The example used a 2D simulation involving a 1D binary grating (or photonic crystal). This tutorial demonstrates how this approach for modeling spatially incoherent dipoles can be extended to cylindrical coordinates for structures with rotational symmetry.
Note: in the case of a disc, the set of dipoles within the quantum well (QW) which spans a 2D surface only needs to be computed along a line. This means that the number of single-dipole simulations necessary for convergence is the same in cylindrical and 3D Cartesian coordinates.
Note: for randomly polarized emission from the QW, each dipole requires computing the emission from the two orthogonal "in-plane" polarization states of and separately and averaging the results in post processing. In this example, only the polarization state is used.
The example uses the same setup as the previous tutorial involving a dielectric disc above a lossless-reflector ground plane. The dipoles are arranged on a line extending from to where is the disc radius. The height of the dipoles ( coordinate) within the disc is fixed. The radiation pattern for a dipole at is computed using a Fourier-series expansion in . The total radiation pattern for an ensemble of incoherent dipoles is just the integral of the individual dipole powers, which we can approximate by a sum:
,
where is a weighting function necessary for ensuring equal contribution from all dipoles relative to the dipole at . Note that a dipole placed exactly at would have zero contribution to the total radiation pattern because its area () is zero. In this example, the dipole at is actually placed at due to an interpolation bug. can be determined empirically by computing the radiation pattern in vacuum for a set of dipoles at different radial positions. The radiation pattern of an dipole in vacuum is which is independent of its position in . This criteria is used to obtain and . (A dependence is expected because a cylindrical delta function should really include a factor in order to integrate to 1 with , but Meep currently does not include this in sources that have zero radial width, and power goes like the square of the current amplitude—therefore, we must include an additional factor to obtain the correct relative power for dipoles at different radii.) This weighting function is also used to sum the flux emitted by each dipole (obtained using using the LDOS feature). This quantity is the denominator in the expression for the extraction efficiency.
This figure shows the radiation pattern from dipoles with of 1.0 m in the middle of a disc of height 0.29 m, radius 1.2 m, and refractive index 2.4. The extraction efficiency for this setup is 0.933517. The runtime is about two hours using two Intel 4.2 GHz Xeon cores.

The simulation script is in examples/disc_extraction_efficiency.py.
import math
from typing import Tuple
import matplotlib.pyplot as plt
import meep as mp
import numpy as np
RESOLUTION_UM = 50
WAVELENGTH_UM = 1.0
N_DISC = 2.4
DISC_RADIUS_UM = 1.2
DISC_THICKNESS_UM = 0.7 * WAVELENGTH_UM / N_DISC
NUM_FARFIELD_PTS = 200
FARFIELD_RADIUS_UM = 1e6 * WAVELENGTH_UM
NUM_DIPOLES = 11
farfield_angles = np.linspace(0, 0.5 * math.pi, NUM_FARFIELD_PTS)
def plot_radiation_pattern_polar(radial_flux: np.ndarray):
"""Plots the radiation pattern in polar coordinates.
Args:
radial_flux: radial flux of the far fields at each angle.
"""
fig, ax = plt.subplots(subplot_kw={"projection": "polar"}, figsize=(6, 6))
ax.plot(
farfield_angles,
radial_flux,
"b-",
)
ax.set_theta_direction(-1)
ax.set_theta_offset(0.5 * math.pi)
ax.set_thetalim(0, 0.5 * math.pi)
ax.grid(True)
ax.set_rlabel_position(22)
ax.set_ylabel("radial flux (a.u.)")
ax.set_title("radiation pattern in polar coordinates")
if mp.am_master():
fig.savefig(
"disc_radiation_pattern_polar.png",
dpi=150,
bbox_inches="tight",
)
def plot_radiation_pattern_3d(radial_flux: np.ndarray):
"""Plots the radiation pattern in 3d Cartesian coordinates.
Args:
radial_flux: radial flux of the far fields at each angle.
"""
phis = np.linspace(0, 2 * np.pi, NUM_FARFIELD_PTS)
xs = np.zeros((NUM_FARFIELD_PTS, NUM_FARFIELD_PTS))
ys = np.zeros((NUM_FARFIELD_PTS, NUM_FARFIELD_PTS))
zs = np.zeros((NUM_FARFIELD_PTS, NUM_FARFIELD_PTS))
for i, theta in enumerate(farfield_angles):
for j, phi in enumerate(phis):
xs[i, j] = radial_flux[i] * np.sin(theta) * np.cos(phi)
ys[i, j] = radial_flux[i] * np.sin(theta) * np.sin(phi)
zs[i, j] = radial_flux[i] * np.cos(theta)
fig, ax = plt.subplots(subplot_kw={"projection": "3d"}, figsize=(6, 6))
ax.plot_surface(xs, ys, zs, cmap="inferno")
ax.set_title("radiation pattern in 3d")
ax.set_box_aspect((np.amax(xs), np.amax(ys), np.amax(zs)))
ax.set_zlabel("radial flux (a.u.)")
ax.set(xticklabels=[], yticklabels=[])
if mp.am_master():
fig.savefig(
"disc_radiation_pattern_3d.png",
dpi=150,
bbox_inches="tight",
)
def radiation_pattern(sim: mp.Simulation, n2f_mon: mp.DftNear2Far) -> np.ndarray:
"""Computes the radiation pattern from the near fields.
Args:
sim: a `Simulation` object.
n2f_mon: a `DftNear2Far` object returned by `Simulation.add_near2far`.
Returns:
The radiation pattern (radial flux at each angle) as a 1d array.
"""
e_field = np.zeros((NUM_FARFIELD_PTS, 3), dtype=np.complex128)
h_field = np.zeros((NUM_FARFIELD_PTS, 3), dtype=np.complex128)
for n in range(NUM_FARFIELD_PTS):
far_field = sim.get_farfield(
n2f_mon,
mp.Vector3(
FARFIELD_RADIUS_UM * math.sin(farfield_angles[n]),
0,
FARFIELD_RADIUS_UM * math.cos(farfield_angles[n]),
),
)
e_field[n, :] = [far_field[j] for j in range(3)]
h_field[n, :] = [far_field[j + 3] for j in range(3)]
flux_x = np.real(
np.conj(e_field[:, 1]) * h_field[:, 2] - np.conj(e_field[:, 2]) * h_field[:, 1]
)
flux_z = np.real(
np.conj(e_field[:, 0]) * h_field[:, 1] - np.conj(e_field[:, 1]) * h_field[:, 0]
)
flux_r = np.sqrt(np.square(flux_x) + np.square(flux_z))
return flux_r
def radiation_pattern_flux(radial_flux: np.ndarray) -> float:
"""Computes the total flux from the radiation pattern.
Based on integrating the radiation pattern over solid angles
spanned by polar angles in the range of [0, π/2].
Args:
radial_flux: radial flux of the far fields at each angle.
"""
dphi = 2 * math.pi
dtheta = farfield_angles[1] - farfield_angles[0]
total_flux = (
np.sum(radial_flux * np.sin(farfield_angles))
* FARFIELD_RADIUS_UM**2
* dtheta
* dphi
)
return total_flux
def dipole_in_disc(zpos: float, rpos_um: float, m: int) -> Tuple[float, np.ndarray]:
"""Computes the total flux and radiation pattern of a dipole in a disc.
Args:
zpos: height of dipole above ground plane as fraction of disc thickness.
rpos_um: radial position of dipole.
m: angular φ dependence of the fields exp(imφ).
Returns:
A 2-tuple of the total flux and the radiation pattern.
"""
pml_um = 1.0 # thickness of PML
padding_um = 1.0 # thickness of air padding above disc
r_um = 4.0 # length of cell in r
frequency = 1 / WAVELENGTH_UM # center frequency of source/monitor
# Runtime termination criteria.
dft_decay_threshold = 1e-4
size_r = r_um + pml_um
size_z = DISC_THICKNESS_UM + padding_um + pml_um
cell_size = mp.Vector3(size_r, 0, size_z)
boundary_layers = [
mp.PML(pml_um, direction=mp.R),
mp.PML(pml_um, direction=mp.Z, side=mp.High),
]
src_pt = mp.Vector3(rpos_um, 0, -0.5 * size_z + zpos * DISC_THICKNESS_UM)
sources = [
mp.Source(
src=mp.GaussianSource(frequency, fwidth=0.05 * frequency),
component=mp.Er,
center=src_pt,
)
]
geometry = [
mp.Block(
material=mp.Medium(index=N_DISC),
center=mp.Vector3(
0.5 * DISC_RADIUS_UM, 0, -0.5 * size_z + 0.5 * DISC_THICKNESS_UM
),
size=mp.Vector3(DISC_RADIUS_UM, mp.inf, DISC_THICKNESS_UM),
)
]
sim = mp.Simulation(
resolution=RESOLUTION_UM,
cell_size=cell_size,
dimensions=mp.CYLINDRICAL,
m=m,
boundary_layers=boundary_layers,
sources=sources,
geometry=geometry,
force_complex_fields=True
)
n2f_mon = sim.add_near2far(
frequency,
0,
1,
mp.FluxRegion(
center=mp.Vector3(0.5 * r_um, 0, 0.5 * size_z - pml_um),
size=mp.Vector3(r_um, 0, 0),
),
mp.FluxRegion(
center=mp.Vector3(
r_um, 0, 0.5 * size_z - pml_um - 0.5 * (padding_um + DISC_THICKNESS_UM)
),
size=mp.Vector3(0, 0, padding_um + DISC_THICKNESS_UM),
),
)
sim.run(
mp.dft_ldos(frequency, 0, 1),
until_after_sources=mp.stop_when_dft_decayed(
tol=dft_decay_threshold,
),
)
delta_vol = 2 * np.pi * rpos_um / (RESOLUTION_UM**2)
dipole_flux = -np.real(sim.ldos_Fdata[0] * np.conj(sim.ldos_Jdata[0])) * delta_vol
dipole_radiation_pattern = radiation_pattern(sim, n2f_mon)
return dipole_flux, dipole_radiation_pattern
if __name__ == "__main__":
dipole_height = 0.5
dipole_rpos_um = np.linspace(0, DISC_RADIUS_UM, NUM_DIPOLES)
delta_rpos_um = DISC_RADIUS_UM / (NUM_DIPOLES - 1)
# 1. Er source at r = 0 requires a single simulation with m = ±1.
# An Er source at r = 0 needs to be slighty offset due to a bug.
# https://github.com/NanoComp/meep/issues/2704
dipole_rpos_um[0] = 1.5 / RESOLUTION_UM
m = -1
dipole_flux, dipole_radiation_pattern = dipole_in_disc(
dipole_height,
dipole_rpos_um[0],
m,
)
flux_total = dipole_flux * dipole_rpos_um[0] * delta_rpos_um
radiation_pattern_total = (
dipole_radiation_pattern * dipole_rpos_um[0] * delta_rpos_um
)
print(
f"dipole:, {dipole_rpos_um[0]:.4f}, "
f"{radiation_pattern_flux(dipole_radiation_pattern):.6f}"
)
# 2. Er source at r > 0 requires Fourier-series expansion of φ.
# Threshold flux to determine when to truncate expansion.
flux_decay_threshold = 1e-2
for rpos_um in dipole_rpos_um[1:]:
dipole_flux_total = 0
dipole_radiation_pattern_total = np.zeros(NUM_FARFIELD_PTS)
dipole_radiation_pattern_flux_max = 0
m = 0
while True:
dipole_flux, dipole_radiation_pattern = dipole_in_disc(
dipole_height, rpos_um, m
)
dipole_flux_total += dipole_flux * (1 if m == 0 else 2)
dipole_radiation_pattern_total += dipole_radiation_pattern * (
1 if m == 0 else 2
)
dipole_radiation_pattern_flux = radiation_pattern_flux(
dipole_radiation_pattern
)
print(
f"dipole:, {rpos_um:.4f}, {m}, " f"{dipole_radiation_pattern_flux:.6f}"
)
if dipole_radiation_pattern_flux > dipole_radiation_pattern_flux_max:
dipole_radiation_pattern_flux_max = dipole_radiation_pattern_flux
if (
m > 0
and (dipole_radiation_pattern_flux / dipole_radiation_pattern_flux_max)
< flux_decay_threshold
):
break
else:
m += 1
dipole_position_scale_factor = 0.5 * (dipole_rpos_um[0] / rpos_um) ** 2
flux_total += (
dipole_flux_total * dipole_position_scale_factor *
rpos_um * delta_rpos_um
)
radiation_pattern_total += (
dipole_radiation_pattern_total * dipole_position_scale_factor *
rpos_um * delta_rpos_um
)
radiation_pattern_total_flux = radiation_pattern_flux(radiation_pattern_total)
extraction_efficiency = radiation_pattern_total_flux / flux_total
print(f"exteff:, {extraction_efficiency:.6f}")
radiation_pattern_scaled = radiation_pattern_total * FARFIELD_RADIUS_UM**2
plot_radiation_pattern_polar(radiation_pattern_scaled)
plot_radiation_pattern_3d(radiation_pattern_scaled)
Focusing Properties of a Metasurface Lens#
This example demonstrates how to compute the far-field profile at the focal length of a metasurface lens. The lens design, which is also part of the tutorial, is based on a supercell of binary-grating unit cells. For a review of the binary-grating geometry as well as a demonstration of computing its phasemap, see Tutorial/Mode Decomposition/Phase Map of a Subwavelength Binary Grating. The far-field calculation of the lens contains two separate components: (1) compute the phasemap of the unit cell as a function of a single geometric parameter, the duty cycle (also referred to as the filling fraction), while keeping its height and periodicity fixed (1.8 μm and 0.3 μm, respectively), and (2) form the supercell lens by tuning the local phase of each of a variable number of unit cells according to the quadratic formula for planar wavefront focusing. The operating wavelength is 0.5 μm and the focal length is 0.2 mm. The input source is an -polarized planewave at normal incidence.
The simulation script is in examples/metasurface_lens.py. The notebook is examples/metasurface_lens.ipynb.
The key to the script is the function grating with three geometric input arguments (periodicity, height, and list of duty cycles) which performs the two main tasks: (1) for a unit cell, it computes the phase (as well as the transmittance) and then translates this value from the range of [-π,π] of Mode Decomposition to [-2π,0] in order to be consistent with the analytic formula for the local phase and (2) for a supercell, it computes the far-field intensity profile around the focal length of the lens.
import meep as mp
import numpy as np
import matplotlib.pyplot as plt
resolution = 50 # pixels/μm
dpml = 1.0 # PML thickness
dsub = 2.0 # substrate thickness
dpad = 2.0 # padding between grating and PML
lcen = 0.5 # center wavelength
fcen = 1/lcen # center frequency
df = 0.2*fcen # frequency width
focal_length = 200 # focal length of metalens
spot_length = 100 # far field line length
ff_res = 10 # far field resolution (points/μm)
k_point = mp.Vector3(0,0,0)
glass = mp.Medium(index=1.5)
pml_layers = [mp.PML(thickness=dpml,direction=mp.X)]
symmetries=[mp.Mirror(mp.Y)]
def grating(gp,gh,gdc_list):
sx = dpml+dsub+gh+dpad+dpml
src_pt = mp.Vector3(-0.5*sx+dpml+0.5*dsub)
mon_pt = mp.Vector3(0.5*sx-dpml-0.5*dpad)
geometry = [mp.Block(material=glass,
size=mp.Vector3(dpml+dsub,mp.inf,mp.inf),
center=mp.Vector3(-0.5*sx+0.5*(dpml+dsub)))]
num_cells = len(gdc_list)
if num_cells == 1:
sy = gp
cell_size = mp.Vector3(sx,sy,0)
sources = [mp.Source(mp.GaussianSource(fcen, fwidth=df),
component=mp.Ez,
center=src_pt,
size=mp.Vector3(y=sy))]
sim = mp.Simulation(resolution=resolution,
cell_size=cell_size,
boundary_layers=pml_layers,
k_point=k_point,
default_material=glass,
sources=sources,
symmetries=symmetries)
flux_obj = sim.add_flux(fcen, 0, 1, mp.FluxRegion(center=mon_pt, size=mp.Vector3(y=sy)))
sim.run(until_after_sources=50)
input_flux = mp.get_fluxes(flux_obj)
sim.reset_meep()
geometry.append(mp.Block(material=glass, size=mp.Vector3(gh,gdc_list[0]*gp,mp.inf), center=mp.Vector3(-0.5*sx+dpml+dsub+0.5*gh)))
sim = mp.Simulation(resolution=resolution,
cell_size=cell_size,
boundary_layers=pml_layers,
geometry=geometry,
k_point=k_point,
sources=sources,
symmetries=symmetries)
flux_obj = sim.add_flux(fcen, 0, 1, mp.FluxRegion(center=mon_pt, size=mp.Vector3(y=sy)))
sim.run(until_after_sources=200)
freqs = mp.get_eigenmode_freqs(flux_obj)
res = sim.get_eigenmode_coefficients(flux_obj, [1], eig_parity=mp.ODD_Z+mp.EVEN_Y)
coeffs = res.alpha
mode_tran = abs(coeffs[0,0,0])**2/input_flux[0]
mode_phase = np.angle(coeffs[0,0,0])
if mode_phase > 0:
mode_phase -= 2*np.pi
return mode_tran, mode_phase
else:
sy = num_cells*gp
cell_size = mp.Vector3(sx,sy,0)
sources = [mp.Source(mp.GaussianSource(fcen, fwidth=df),
component=mp.Ez,
center=src_pt,
size=mp.Vector3(y=sy))]
for j in range(num_cells):
geometry.append(mp.Block(material=glass,
size=mp.Vector3(gh,gdc_list[j]*gp,mp.inf),
center=mp.Vector3(-0.5*sx+dpml+dsub+0.5*gh,-0.5*sy+(j+0.5)*gp)))
sim = mp.Simulation(resolution=resolution,
cell_size=cell_size,
boundary_layers=pml_layers,
geometry=geometry,
k_point=k_point,
sources=sources,
symmetries=symmetries)
n2f_obj = sim.add_near2far(fcen, 0, 1, mp.Near2FarRegion(center=mon_pt, size=mp.Vector3(y=sy)))
sim.run(until_after_sources=500)
return abs(sim.get_farfields(n2f_obj, ff_res, center=mp.Vector3(-0.5*sx+dpml+dsub+gh+focal_length), size=mp.Vector3(spot_length))['Ez'])**2
In the first of two parts of the calculation, a phasemap of the binary-grating unit cell is generated based on varying the duty cycle from 0.1 to 0.9.
gp = 0.3 # grating periodicity
gh = 1.8 # grating height
gdc = np.linspace(0.1,0.9,30) # grating duty cycle
mode_tran = np.empty((gdc.size))
mode_phase = np.empty((gdc.size))
for n in range(gdc.size):
mode_tran[n], mode_phase[n] = grating(gp,gh,[gdc[n]])
plt.figure(dpi=200)
plt.subplot(1,2,1)
plt.plot(gdc, mode_tran, 'bo-')
plt.xlim(gdc[0],gdc[-1])
plt.xticks([t for t in np.linspace(0.1,0.9,5)])
plt.xlabel("grating duty cycle")
plt.ylim(0.96,1.00)
plt.yticks([t for t in np.linspace(0.96,1.00,5)])
plt.title("transmittance")
plt.subplot(1,2,2)
plt.plot(gdc, mode_phase, 'rs-')
plt.grid(True)
plt.xlim(gdc[0],gdc[-1])
plt.xticks([t for t in np.linspace(0.1,0.9,5)])
plt.xlabel("grating duty cycle")
plt.ylim(-2*np.pi,0)
plt.yticks([t for t in np.linspace(-6,0,7)])
plt.title("phase (radians)")
plt.tight_layout(pad=0.5)
plt.show()
The phasemap is shown below. The left figure shows the transmittance which is nearly unity for all values of the duty cycle; the Fresnel transmittance is 0.96 for the glass-air interface. This is expected since the periodicity is subwavelength. The right figure shows the phase. There is a subregion in the middle of the plot spanning the duty-cycle range of roughly 0.16 to 0.65 in which the phase varies continuously over the full range of -2π to 0. This structural regime is used to design the supercell lens.

In the second part of the calculation, the far-field energy-density profile of three supercell lens designs, comprised of 201, 401, and 801 unit cells, are computed using the quadratic formula for the local phase. Initially, this involves fitting the unit-cell phase data to a finer duty-cycle grid in order to enhance the local-phase interpolation of the supercell. This is important since as the number of unit cells in the lens increases, the local phase via the duty cycle varies more gradually from unit cell to unit cell. However, if the duty cycle becomes too gradual (i.e., less than a tenth of the pixel dimensions), the resolution may also need to be increased in order to improve the accuracy of subpixel smoothing.
gdc_new = np.linspace(0.16,0.65,500)
mode_phase_interp = np.interp(gdc_new, gdc, mode_phase)
print("phase-range:, {:.6f}".format(mode_phase_interp.max()-mode_phase_interp.min()))
phase_tol = 1e-2
num_cells = [100,200,400]
ff_nc = np.empty((spot_length*ff_res,len(num_cells)))
for k in range(len(num_cells)):
gdc_list = []
for j in range(-num_cells[k],num_cells[k]+1):
phase_local = 2*np.pi/lcen * (focal_length-((j*gp)**2 + focal_length**2)**0.5) # local phase at the center of the j'th unit cell
phase_mod = phase_local % (-2*np.pi) # restrict phase to [-2*pi,0]
if phase_mod > mode_phase_interp.max():
phase_mod = mode_phase_interp.max()
if phase_mod < mode_phase_interp.min():
phase_mod = mode_phase_interp.min()
idx = np.transpose(np.nonzero(np.logical_and(mode_phase_interp > phase_mod-phase_tol, mode_phase_interp < phase_mod+phase_tol)))
gdc_list.append(gdc_new[idx[0][0]])
ff_nc[:,k] = grating(gp,gh,gdc_list)
x = np.linspace(focal_length-0.5*spot_length,focal_length+0.5*spot_length,ff_res*spot_length)
plt.figure(dpi=200)
plt.semilogy(x,abs(ff_nc[:,0])**2,'bo-',label='num_cells = {}'.format(2*num_cells[0]+1))
plt.semilogy(x,abs(ff_nc[:,1])**2,'ro-',label='num_cells = {}'.format(2*num_cells[1]+1))
plt.semilogy(x,abs(ff_nc[:,2])**2,'go-',label='num_cells = {}'.format(2*num_cells[2]+1))
plt.xlabel('x coordinate (μm)')
plt.ylabel(r'energy density of far-field electric fields, |E$_z$|$^2$')
plt.title('focusing properties of a binary-grating metasurface lens')
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()
Shown below is the supercell lens design involving 201 unit cells. Note that even though periodic boundaries are used in the supercell calculation (via the k_point), the choice of cell boundaries in the y (or longitudinal) direction is irrelevant given the finite length of the lens. For example, PMLs could also have been used (at the expense of a larger cell). Although add_near2far does support periodic boundaries (via the nperiods parameter), it is not necessary for this particular example.

The far-field energy-density profile is shown below for the three lens designs. As the number of unit cells increases, the focal spot becomes sharper and sharper. This is expected since the longer the focal length, the bigger the lens required to demonstrate focusing (which means more unit cells). In this example, the largest lens design contains 801 unit cells which corresponds to 0.24 mm or 1.2X the focal length.

Diffraction Spectrum of a Finite Binary Grating#
In this example, we compute the diffraction spectrum of a binary phase grating with finite length. To compute the diffraction spectrum of the infinite periodic structure requires mode decomposition; for a demonstration, see Tutorial/Mode Decomposition/Diffraction Spectrum of a Binary Grating which also describes the grating geometry used in this example (i.e., periodicity of 10 μm, height of 0.5 μm, duty cycle of 0.5, and index 1.5 in air). Note that an infinite periodic structure actually has no spatial separation of the diffracted orders; they are all present at every far-field point. The focus of this tutorial is to demonstrate add_near2far's support for periodic boundaries.
The simulation script is in examples/binary_grating_n2f.py. The notebook is examples/binary_grating_n2f.ipynb.
The simulation involves computing the scattered near fields of a finite-length grating for an -polarized, pulsed planewave source spanning wavelengths of 0.4-0.6 μm at normal incidence. The far fields are then computed for 500 points along a line parallel to the grating axis positioned 100 m away (i.e., , the Fraunhofer distance; where is the number of unit cells and is the grating periodicity, is the source wavelength) in the upper half plane of the symmetric finite structure with length corresponding to a 20° cone. The diffraction spectra is computed as the ratio of the energy density of the far fields from two separate runs: (1) an empty cell to obtain the fields from just the incident planewave and (2) a binary-grating unit cell to obtain the scattered fields.
Modeling a finite grating requires specifying the nperiods parameter of add_near2far which sums 2*nperiods+1 Bloch-periodic copies of the near fields. However, because of the way in which the edges of the structure are handled, this approach is only an approximation for a finite periodic surface. We will verify that the error from this approximation is (1/nperiods) by comparing its result with that of a true finite periodic structure involving multiple periods in a supercell arrangement terminated with a flat surface extending into PML. (There are infinitely many ways to terminate a finite periodic structure, of course, and different choices will have slightly different errors compared to the periodic approximation.)
import meep as mp
import math
import numpy as np
from numpy import linalg as LA
import matplotlib.pyplot as plt
resolution = 25 # pixels/μm
dpml = 1.0 # PML thickness
dsub = 3.0 # substrate thickness
dpad = 3.0 # padding between grating and PML
gp = 10.0 # grating period
gh = 0.5 # grating height
gdc = 0.5 # grating duty cycle
nperiods = 10 # number of unit cells in finite periodic grating
ff_distance = 1e8 # far-field distance from near-field monitor
ff_angle = 20 # far-field cone angle
ff_npts = 500 # number of far-field points
ff_length = ff_distance*math.tan(math.radians(ff_angle))
ff_res = ff_npts/ff_length
sx = dpml+dsub+gh+dpad+dpml
cell_size = mp.Vector3(sx)
pml_layers = [mp.PML(thickness=dpml,direction=mp.X)]
symmetries = [mp.Mirror(mp.Y)]
wvl_min = 0.4 # min wavelength
wvl_max = 0.6 # max wavelength
fmin = 1/wvl_max # min frequency
fmax = 1/wvl_min # max frequency
fcen = 0.5*(fmin+fmax) # center frequency
df = fmax-fmin # frequency width
src_pt = mp.Vector3(-0.5*sx+dpml+0.5*dsub)
sources = [mp.Source(mp.GaussianSource(fcen, fwidth=df), component=mp.Ez, center=src_pt)]
k_point = mp.Vector3()
glass = mp.Medium(index=1.5)
sim = mp.Simulation(resolution=resolution,
cell_size=cell_size,
boundary_layers=pml_layers,
k_point=k_point,
default_material=glass,
sources=sources)
nfreq = 21
n2f_pt = mp.Vector3(0.5*sx-dpml-0.5*dpad)
n2f_obj = sim.add_near2far(fcen, df, nfreq, mp.Near2FarRegion(center=n2f_pt))
sim.run(until_after_sources=mp.stop_when_fields_decayed(50, mp.Ez, n2f_pt, 1e-9))
ff_source = sim.get_farfields(n2f_obj, ff_res, center=mp.Vector3(ff_distance,0.5*ff_length), size=mp.Vector3(y=ff_length))
sim.reset_meep()
### unit cell with periodic boundaries
sy = gp
cell_size = mp.Vector3(sx,sy)
sources = [mp.Source(mp.GaussianSource(fcen, fwidth=df), component=mp.Ez, center=src_pt, size=mp.Vector3(y=sy))]
geometry = [mp.Block(material=glass, size=mp.Vector3(dpml+dsub,mp.inf,mp.inf), center=mp.Vector3(-0.5*sx+0.5*(dpml+dsub))),
mp.Block(material=glass, size=mp.Vector3(gh,gdc*gp,mp.inf), center=mp.Vector3(-0.5*sx+dpml+dsub+0.5*gh))]
sim = mp.Simulation(resolution=resolution,
split_chunks_evenly=True,
cell_size=cell_size,
boundary_layers=pml_layers,
geometry=geometry,
k_point=k_point,
sources=sources,
symmetries=symmetries)
n2f_obj = sim.add_near2far(fcen, df, nfreq, mp.Near2FarRegion(center=n2f_pt, size=mp.Vector3(y=sy)), nperiods=nperiods)
sim.run(until_after_sources=mp.stop_when_fields_decayed(50, mp.Ez, n2f_pt, 1e-9))
ff_unitcell = sim.get_farfields(n2f_obj, ff_res, center=mp.Vector3(ff_distance,0.5*ff_length), size=mp.Vector3(y=ff_length))
sim.reset_meep()
### finite periodic grating with flat surface termination extending into PML
num_cells = 2*nperiods+1
sy = dpml+num_cells*gp+dpml
cell_size = mp.Vector3(sx,sy)
pml_layers = [mp.PML(thickness=dpml)]
sources = [mp.Source(mp.GaussianSource(fcen, fwidth=df, is_integrated=True),
component=mp.Ez,
center=src_pt,
size=mp.Vector3(y=sy))]
geometry = [mp.Block(material=glass, size=mp.Vector3(dpml+dsub,mp.inf,mp.inf), center=mp.Vector3(-0.5*sx+0.5*(dpml+dsub)))]
for j in range(num_cells):
geometry.append(mp.Block(material=glass,
size=mp.Vector3(gh,gdc*gp,mp.inf),
center=mp.Vector3(-0.5*sx+dpml+dsub+0.5*gh,-0.5*sy+dpml+(j+0.5)*gp)))
sim = mp.Simulation(resolution=resolution,
split_chunks_evenly=True,
cell_size=cell_size,
boundary_layers=pml_layers,
geometry=geometry,
k_point=k_point,
sources=sources,
symmetries=symmetries)
n2f_obj = sim.add_near2far(fcen, df, nfreq, mp.Near2FarRegion(center=n2f_pt, size=mp.Vector3(y=sy-2*dpml)))
sim.run(until_after_sources=mp.stop_when_fields_decayed(50, mp.Ez, n2f_pt, 1e-9))
ff_supercell = sim.get_farfields(n2f_obj, ff_res, center=mp.Vector3(ff_distance,0.5*ff_length), size=mp.Vector3(y=ff_length))
norm_err = LA.norm(ff_unitcell['Ez']-ff_supercell['Ez'])/nperiods
print("error:, {}, {}".format(nperiods,norm_err))
A plot of (a) the diffraction/far-field spectra and (b) its cross section at a fixed wavelength of 0.5 μm, is generated using the commands below and shown in the accompanying figure for two cases: (1) nperiods = 1 (no tiling; default) and (2) nperiods = 10 (21 copies). Note that because the evenly-spaced points on the line used to compute the far fields are mapped to angles in the plot, the angular data is not evenly spaced. A similar non-uniformity occurs when transforming the far-field data from the frequency to wavelength domain.
freqs = mp.get_near2far_freqs(n2f_obj)
wvl = np.divide(1,freqs)
ff_lengths = np.linspace(0,ff_length,ff_npts)
angles = [math.degrees(math.atan(f)) for f in ff_lengths/ff_distance]
wvl_slice = 0.5
idx_slice = np.where(np.asarray(freqs) == 1/wvl_slice)[0][0]
rel_enh = np.absolute(ff_unitcell['Ez'])**2/np.absolute(ff_source['Ez'])**2
plt.figure(dpi=150)
plt.subplot(1,2,1)
plt.pcolormesh(wvl,angles,rel_enh,cmap='Blues',shading='flat')
plt.axis([wvl_min,wvl_max,0,ff_angle])
plt.xlabel("wavelength (μm)")
plt.ylabel("angle (degrees)")
plt.grid(linewidth=0.5,linestyle='--')
plt.xticks([t for t in np.arange(wvl_min,wvl_max+0.1,0.1)])
plt.yticks([t for t in range(0,ff_angle+1,10)])
plt.title("far-field spectra")
plt.subplot(1,2,2)
plt.plot(angles,rel_enh[:,idx_slice],'bo-')
plt.xlim(0,ff_angle)
plt.ylim(0)
plt.xticks([t for t in range(0,ff_angle+1,10)])
plt.xlabel("angle (degrees)")
plt.ylabel("relative enhancement")
plt.grid(axis='x',linewidth=0.5,linestyle='--')
plt.title("f.-f. spectra @ λ = {:.1} μm".format(wvl_slice))
plt.tight_layout(pad=0.5)
plt.show()

For the case of nperiods = 1, three diffraction orders are present in the far-field spectra as broad peaks with finite angular width (a fourth peak/order is also visible). When nperiods = 10, the diffraction orders become sharp, narrow peaks. The three diffraction orders are labeled in the right inset of the bottom figure as m=1, 3, and 5 corresponding to angles 2.9°, 8.6°, and 14.5° which, along with the diffraction efficiency, can be computed analytically using scalar theory as described in Tutorial/Mode Decomposition/Diffraction Spectrum of a Binary Grating. As an additional validation of the simulation results, the ratio of any two diffraction peaks () is consistent with that of its diffraction efficiencies: .
We verify that the error in add_near2far — defined as the -norm of the difference of the two far-field datasets from the unit- and super-cell calculations normalized by nperiods — is (1/nperiods) by comparing results for three values of nperiods: 5, 10, and 20. The error values, which are displayed in the output in the line prefixed by error:, are: 0.0001195599054639075, 5.981324591508146e-05, and 2.989829913961854e-05. The pairwise ratios of these errors is nearly 2 as expected (i.e., doubling nperiods results in halving the error).
For a single process, the far-field calculation in both runs takes roughly the same amount of time. The wall-clock time is indicated by the getting farfields category of the Field time usage statistics displayed as part of the output after time stepping is complete. Time-stepping a supercell, however, which for nperiods=20 is more than 41 times larger than the unit cell (because of the PML termination) results in a total wall-clock time that is more than 40% larger. The slowdown is also due to the requirement of computing 41 times as many Fourier-transformed near fields. Thus, in the case of the unit-cell simulation, the reduced accuracy is a tradeoff for shorter runtime and less storage. In this example which involves multiple output wavelengths, the time for the far-field calculation can be reduced further on a single, shared-memory, multi-core machine via multithreading by compiling Meep with OpenMP and specifying the environment variable OMP_NUM_THREADS to be an integer greater than one prior to execution.
Finally, we can validate the results for the diffraction spectra of a finite grating via a different approach than computing the far fields: as the (spatial) Fourier transform of the scattered fields. This involves two simulations — one with the grating and the other with just a flat surface — and subtracting the Fourier-transformed fields at a given frequency from the two runs to obtain the scattered fields . The Fourier transform of the scattered fields is then computed in post processing: , where is the amplitude of the corresponding Fourier component. For a grating with periodicity , we should expect to see peaks in the diffraction spectra at for The total number of diffraction orders is determined by the wavelength as described in Tutorial/Mode Decomposition/Transmittance Spectra for Planewave at Normal Incidence.
The simulation setup is shown in the schematic below. The binary grating has μm at a wavelength of 0.5 μm via a normally-incident planewave pulse (which must extend into the PML region in order to span the entire width of the cell). The grating structure is terminated with a flat-surface padding in order to give the scattered field space to decay at the edge of the cell.

The simulation script is in examples/finite_grating.py. The notebook is examples/finite_grating.ipynb.
import meep as mp
import numpy as np
import math
import matplotlib.pyplot as plt
# True: plot the scattered fields in the air region adjacent to the grating
# False: plot the diffraction spectra based on a 1d cross section of the scattered fields
field_profile = True
resolution = 50 # pixels/μm
dpml = 1.0 # PML thickness
dsub = 2.0 # substrate thickness
dpad = 1.0 # flat-surface padding
gp = 1.0 # grating periodicity
gh = 0.5 # grating height
gdc = 0.5 # grating duty cycle
num_cells = 5 # number of grating unit cells
# air region thickness adjacent to grating
dair = 10 if field_profile else dpad
wvl = 0.5 # center wavelength
fcen = 1/wvl # center frequency
k_point = mp.Vector3()
glass = mp.Medium(index=1.5)
pml_layers = [mp.PML(thickness=dpml)]
symmetries=[mp.Mirror(mp.Y)]
sx = dpml+dsub+gh+dair+dpml
sy = dpml+dpad+num_cells*gp+dpad+dpml
cell_size = mp.Vector3(sx,sy)
src_pt = mp.Vector3(-0.5*sx+dpml+0.5*dsub)
sources = [mp.Source(mp.GaussianSource(fcen,fwidth=0.2*fcen,is_integrated=True),
component=mp.Ez,
center=src_pt,
size=mp.Vector3(y=sy))]
geometry = [mp.Block(material=glass,
size=mp.Vector3(dpml+dsub,mp.inf,mp.inf),
center=mp.Vector3(-0.5*sx+0.5*(dpml+dsub)))]
sim = mp.Simulation(resolution=resolution,
cell_size=cell_size,
boundary_layers=pml_layers,
geometry=geometry,
k_point=k_point,
sources=sources,
symmetries=symmetries)
mon_pt = mp.Vector3(0.5*sx-dpml-0.5*dair)
near_fields = sim.add_dft_fields([mp.Ez], fcen, 0, 1, center=mon_pt, size=mp.Vector3(dair if field_profile else 0,sy-2*dpml))
sim.run(until_after_sources=100)
flat_dft = sim.get_dft_array(near_fields, mp.Ez, 0)
sim.reset_meep()
for j in range(num_cells):
geometry.append(mp.Block(material=glass,
size=mp.Vector3(gh,gdc*gp,mp.inf),
center=mp.Vector3(-0.5*sx+dpml+dsub+0.5*gh,-0.5*sy+dpml+dpad+(j+0.5)*gp)))
sim = mp.Simulation(resolution=resolution,
cell_size=cell_size,
boundary_layers=pml_layers,
geometry=geometry,
k_point=k_point,
sources=sources,
symmetries=symmetries)
near_fields = sim.add_dft_fields([mp.Ez], fcen, 0, 1, center=mon_pt, size=mp.Vector3(dair if field_profile else 0,sy-2*dpml))
sim.run(until_after_sources=100)
grating_dft = sim.get_dft_array(near_fields, mp.Ez, 0)
scattered_field = grating_dft-flat_dft
scattered_amplitude = np.abs(scattered_field)**2
[x,y,z,w] = sim.get_array_metadata(dft_cell=near_fields)
if field_profile:
if mp.am_master():
plt.figure(dpi=150)
plt.pcolormesh(x,y,np.rot90(scattered_amplitude),cmap='inferno',shading='gouraud',vmin=0,vmax=scattered_amplitude.max())
plt.gca().set_aspect('equal')
plt.xlabel('x (μm)')
plt.ylabel('y (μm)')
# ensure that the height of the colobar matches that of the plot
from mpl_toolkits.axes_grid1 import make_axes_locatable
divider = make_axes_locatable(plt.gca())
cax = divider.append_axes("right", size="5%", pad=0.05)
plt.colorbar(cax=cax)
plt.tight_layout()
plt.show()
else:
ky = np.fft.fftshift(np.fft.fftfreq(len(scattered_field), 1/resolution))
FT_scattered_field = np.fft.fftshift(np.fft.fft(scattered_field))
if mp.am_master():
plt.figure(dpi=150)
plt.subplots_adjust(hspace=0.3)
plt.subplot(2,1,1)
plt.plot(y,scattered_amplitude,'bo-')
plt.xlabel("y (μm)")
plt.ylabel("field amplitude")
plt.subplot(2,1,2)
plt.plot(ky,np.abs(FT_scattered_field)**2,'ro-')
plt.gca().ticklabel_format(axis='y',style='sci',scilimits=(0,0))
plt.xlabel(r'wavevector k$_y$, 2π (μm)$^{-1}$')
plt.ylabel("Fourier transform")
plt.gca().set_xlim([-3, 3])
plt.tight_layout(pad=1.0)
plt.show()
Results are shown for two finite gratings with 5 and 20 periods.


The scattered field amplitude profile (the top figure in each of the two sets of results) shows that the fields decay to zero away from the grating (which is positioned at the left edge of the figure in the region indicated by the bright spots). The middle figure is the field amplitude along a 1d slice above the grating (marked by the dotted green line in the top figure). Note the decaying fields at the edges due to the flat-surface termination. The bottom figure is the Fourier transform of the fields from the 1d slice. As expected, there are only three diffraction orders present at for . These peaks are becoming sharper as the number of grating periods increases.
The sharpness of the peaks directly corresponds to how collimated the diffracted beams are, and in the limit of infinitely many periods the resulting -function peaks correspond to diffracted planewaves. (The squared amplitude of each peak is proportional to the power in the corresponding diffraction order.) One can also obtain the collimation of the beams more directly by using Meep's near2far feature to compute the far-field diffracted waves — this approach is more straightforward, but potentially much more expensive than looking at the Fourier transform of the near field, because one may need a large number of far-field points to resolve the full diffracted beams. In general, there is a tradeoff in computational science between doing direct "numerical experiments" that are conceptually straightforward but often expensive, versus more indirect and tricky calculations that don't directly correspond to laboratory experiments but which can sometimes be vastly more efficient at extracting physical information.
In 3d, the procedure is very similar, but a little more effort is required to disentangle the two polarizations relative to the plane of incidence [the plane for each Fourier component ]. For propagation in the direction, you would Fourier transform both and of the scattered field as a function of . For each , you decompose the corresponding into the amplitude parallel to [which gives the polarization amplitude if you multiply by , where , is the refractive index of the ambient medium, and is the angular frequency; is the outgoing angle, where is normal] and perpendicular to [which equals the polarization amplitude]. Then square these amplitudes to get something proportional to power as above. (Note that this analysis is the same even if the incident wave is at an oblique angle, although the k locations of the diffraction peaks will change.) Simulating large finite gratings is usually unnecessary since the accuracy improvements are negligible. For example, a 3d simulation of a finite grating with e.g. 100 periods by 100 periods which is computationally expensive would only provide a tiny correction of ~1% (on par with fabrication errors) compared to the infinite structure involving a single unit cell. A finite grating with a small number of periods (e.g., 5 or 10) exhibits weak diffractive effects and is therefore not considered a diffractive grating.
Truncation Errors from a Non-Closed Near-Field Surface#
For this demonstration, we will compute the far-field spectra of a resonant cavity mode in a holey waveguide (a structure introduced in Tutorial/Resonant Modes and Transmission in a Waveguide Cavity) and demonstrate that these fields are exactly equivalent to the actual DFT fields at the same location. A schematic of the simulation setup generated using plot2D is shown below.
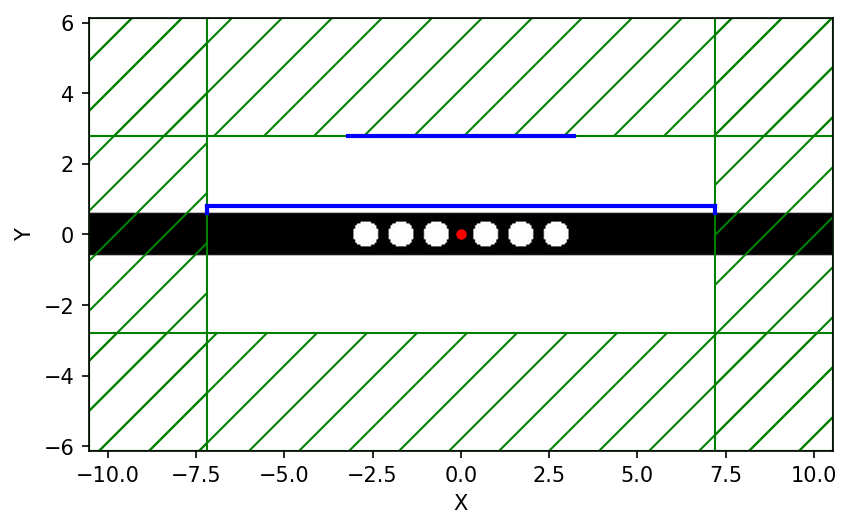
The script is in examples/cavity-farfield.py. The notebook is examples/cavity-farfield.ipynb.
import meep as mp
import numpy as np
import matplotlib
matplotlib.use('agg')
import matplotlib.pyplot as plt
resolution = 20 # pixels/μm
fcen = 0.25 # pulse center frequency
df = 0.2 # pulse width (in frequency)
eps = 13 # dielectric constant of waveguide
w = 1.2 # width of waveguide
r = 0.36 # radius of holes
d = 1.4 # defect spacing (ordinary spacing = 1)
N = 3 # number of holes on either side of defect
dpad = 32 # padding between last hole and PML edge
dpml = 0.5/(fcen-0.5*df) # PML thickness (> half the largest wavelength)
sx = 2*(dpad+dpml+N) + d - 1 # size of cell in x direction
d1 = 0.2 # y-distance from waveguide edge to near2far surface
d2 = 2.0 # y-distance from near2far surface to far-field line
sy = w + 2*(d1+d2+dpml) # size of cell in y direction (perpendicular to wvg.)
cell = mp.Vector3(sx,sy,0)
geometry = [mp.Block(center=mp.Vector3(),
size=mp.Vector3(mp.inf, w, mp.inf),
material=mp.Medium(epsilon=eps))]
for i in range(N):
geometry.append(mp.Cylinder(r, center=mp.Vector3(d / 2 + i)))
geometry.append(mp.Cylinder(r, center=mp.Vector3(d / -2 - i)))
pml_layers = [mp.PML(dpml)]
sources = [mp.Source(src=mp.GaussianSource(fcen, fwidth=df),
component=mp.Hz,
center=mp.Vector3())]
symmetries = [mp.Mirror(mp.X, phase=-1),
mp.Mirror(mp.Y, phase=-1)]
sim = mp.Simulation(cell_size=cell,
geometry=geometry,
sources=sources,
symmetries=symmetries,
boundary_layers=pml_layers,
resolution=resolution)
nearfield = sim.add_near2far(
fcen, 0, 1,
mp.Near2FarRegion(mp.Vector3(0, 0.5*w + d1),
size=mp.Vector3(sx - 2*dpml)),
mp.Near2FarRegion(mp.Vector3(-0.5*sx + dpml, 0.5*w + 0.5*d1),
size=mp.Vector3(0, d1),
weight=-1.0),
mp.Near2FarRegion(mp.Vector3(0.5*sx - dpml, 0.5*w + 0.5*d1),
size=mp.Vector3(0, d1)),
)
mon = sim.add_dft_fields(
[mp.Hz],
fcen,
0,
1,
center=mp.Vector3(0, 0.5*w + d1 + d2),
size=mp.Vector3(sx - 2*(dpad+dpml), 0)
)
sim.run(until_after_sources=mp.stop_when_dft_decayed())
sim.plot2D()
if mp.am_master():
plt.savefig(f'cavity_farfield_plot2D_dpad{dpad}_{d1}_{d2}.png',bbox_inches='tight',dpi=150)
Hz_mon = sim.get_dft_array(mon, mp.Hz, 0)
(x,y,z,w) = sim.get_array_metadata(dft_cell=mon)
ff = []
for xc in x:
ff_pt = sim.get_farfield(nearfield, mp.Vector3(xc,y[0]))
ff.append(ff_pt[5])
ff = np.array(ff)
if mp.am_master():
plt.figure()
plt.subplot(1,3,1)
plt.plot(x,np.real(Hz_mon),'bo-',label='DFT')
plt.plot(x,np.real(ff),'ro-',label='N2F')
plt.legend()
plt.xlabel('$x$ (μm)')
plt.ylabel('real(Hz)')
plt.subplot(1,3,2)
plt.plot(x,np.imag(Hz_mon),'bo-',label='DFT')
plt.plot(x,np.imag(ff),'ro-',label='N2F')
plt.legend()
plt.xlabel('$x$ (μm)')
plt.ylabel('imag(Hz)')
plt.subplot(1,3,3)
plt.plot(x,np.abs(Hz_mon),'bo-',label='DFT')
plt.plot(x,np.abs(ff),'ro-',label='N2F')
plt.legend()
plt.xlabel('$x$ (μm)')
plt.ylabel('|Hz|')
plt.suptitle(f'comparison of near2far and actual DFT fields\n dpad={dpad}, d1={d1}, d2={d2}')
plt.subplots_adjust(wspace=0.6)
plt.savefig(f'test_Hz_dft_vs_n2f_res{resolution}_dpad{dpad}_d1{d1}_d2{d2}.png',
bbox_inches='tight',
dpi=150)
Because of the adjoining waveguides, the total structure is actually infinitely extended in the direction. It is therefore not possible in a finite simulation to define a closed near-field surface for capturing all outgoing waves in the top-half of the cell because (currently) the near-field surface cannot be extended into the PML. The only workaround is to make the computational cell and hence the near-field surface sufficiently wide so that the truncation effect is negligible, ideally also fine-tuning the distance between the near-field surface and the waveguide mode as discussed below.
A non-closed near-field surface introduces two types of errors from the truncation:
- If an infinite near-field surface is positioned adjacent to the guided mode, the equivalent currents on that surface do not radiate any fields simply because the guided mode is under the light cone. However, if the near-field surface is truncated to a finite length, the equivalent currents do radiate from the edges. This windowing/truncation is equivalent to "smearing out" guided modes in Fourier space (convolving with a sinc function) so that the currents have radiative Fourier components inside light cone.
- If the finite/truncated near-field surface is moved farther away from the waveguide along the direction (
d1parameter in the script), then the spurious radiation from the guided mode decreases exponentially fast. However, if the surface is moved too far away (i.e.,d1), then it will fail to capture more and more of the radiation from the cavity mode and this will make the results less accurate.
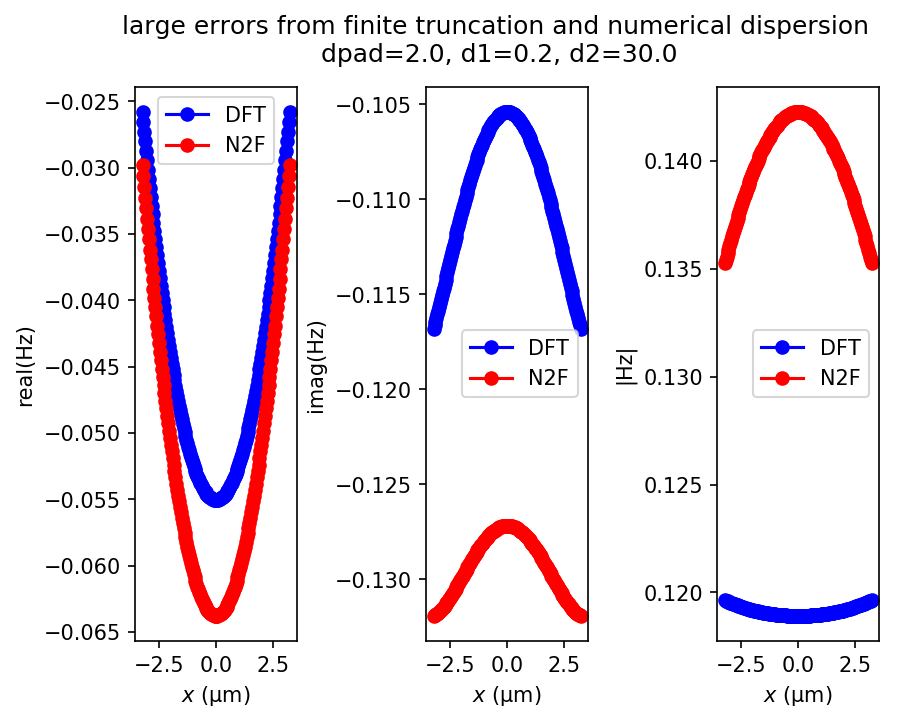
A closed near-field surface will still disagree with a brute-force far-field calculation at a finite resolution, because of discretization errors (the near-to-far transform uses the analytical Green's function of the exact Maxwell equations, not the discretized Green's function), although these errors decrease with spatial resolution. The biggest of these discretization effects is numerical dispersion (described in Chapter 4 of Taflove and Hagness, 2005), in which the phase velocity is slightly different between the exact and discretized equations. In consequence, a brute-force far-field calculation has phase errors that grow with the propagation distance (the d2 parameter in the script).
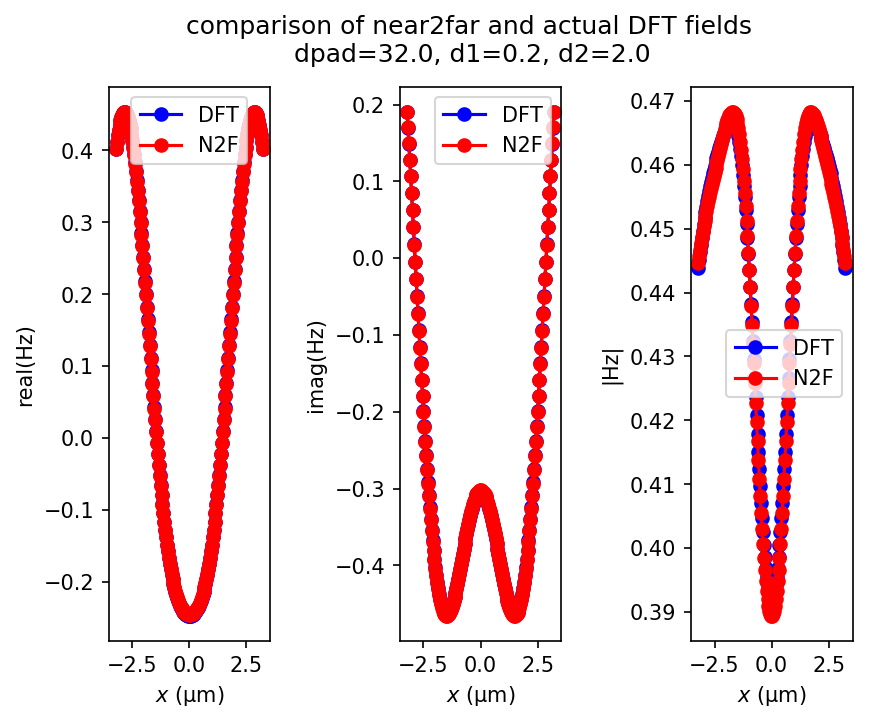
In this example, to demonstrate agreement between the far fields and DFT fields, there are two requirements: (1) the cell size in the direction via dpad needs to be sufficiently large in order to minimize the impact of the spurious radiation from the edge of the near-field surface and (2) the far-field region needs to be sufficiently close to the near-field surface to minimize discrepancies caused by numerical dispersion.
When these two conditions are not met as in the example below involving a small dpad and large d2, the error from the finite truncation and numerical dispersion can be large and therefore result in a significant mismatch between the far fields computed using the near-to-far field transformation versus the actual DFT fields at the same location.