Chunks and Symmetry#
As described in Computer Physics Communications, Vol. 181, pp. 687-702 (2010),
Meep subdivides geometries into chunks. Each chunk is a contiguous region of space — a line, rectangle, or parallelepiped for 1d/2d/3d Cartesian geometries, or an annular section in a cylindrical geometry—whose sizes are automatically determined by libmeep. In parallel calculations, each chunk is assigned, in its entirety, to precisely one process — that is, no chunk exists partly on one processor and partly on another.
Many internal operations in Meep consist of looping over points in the
Yee grid, generally performing some operation involving the field
components and material parameters at each point.
In principle, this involves nested for loops; in practice,
it is complicated by several factors, including the following:
-
For calculations that exploit symmetry, only a portion of the full grid is actually stored in memory, and obtaining values for field components at a point that isn't stored requires a tricky procedure discussed below.
-
Similarly, for Bloch-periodic geometries, only grid points in the unit cell are stored, but we may want the fields at a point lying outside the unit cell, again requiring a bit of a shell game to process correctly.
-
Because of the staggered nature of the Yee grid, "looping over grid points" can mean multiple things — are we visiting only E-field sites, or only H-field sites, or both? Either way, obtaining a full set of field-component values at any one grid point necessarily involves a certain average over neighboring grid points.
To shield developers from the need to grapple with these complications
when implementing loops over grid points, libmeep provides
a convenient routine called loop_in_chunks and a set of macros
that take care of many of the above hassles. This is discussed in more
detail below.
Chunk Data Structures#
For each chunk in a geometry, libmeep creates instances of
the data structures structure_chunk (storing data on the
geometry of the chunk and the material properties at grid
points in the chunk) and fields_chunk (storing the actual values
of the time-domain field components at grid points in the chunk).
Frequency-domain (DFT) field components are handled by a separate
data structure called dft_chunk. Each instance of dft_chunk
is associated with a single instance of fields_chunk (namely,
whichever one stores the time-domain fields at the grid points
covered by the DFT chunk); however, because DFT fields are typically
only tabulated on a subset of the full grid, the grid volume
covered by a dft_chunk may be only a subset of the volume
covered by its parent fields_chunk, and not all fields_chunks
have dft_chunks associated with them.
Chunking of a 2d Geometry#
Our running example throughout this page will be a 2d geometry, of dimensions , with PML layers of thickness 1 on all sides, discretized with 5 points per unit length to yield a 40 × 30 grid.
Chunking in the Single-Processor Case#
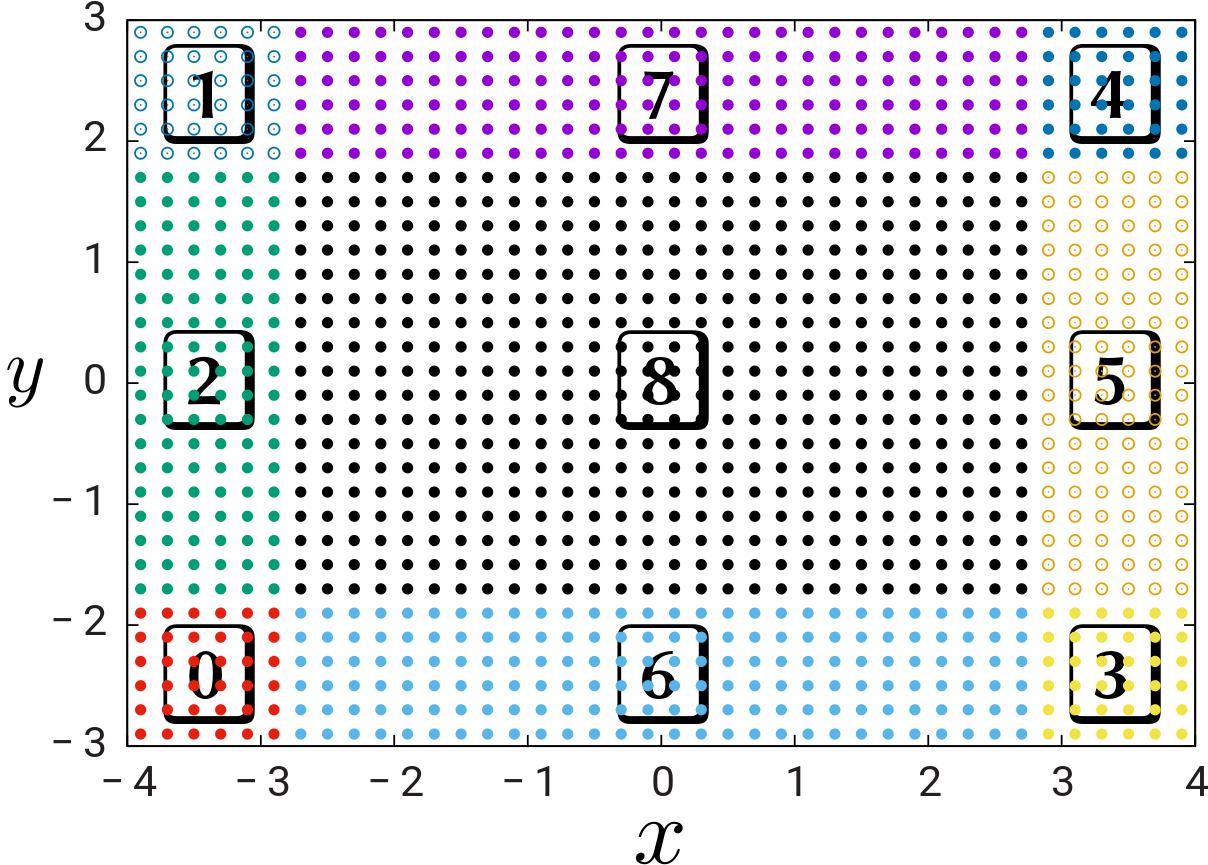
In a single-processor run, libmeep subdivides this geometry
into 9 chunks (click for larger image):
The width of the 8 chunks around the perimeter is set by the PML thickness.
Note that the chunks are not of uniform sizes and that their ordering is somewhat arbitrary. In particular, consecutive chunks are not necessarily adjacent.
Chunk Statistics#
As noted above, each chunk is a contiguous region of space defined
by a Cartesian product of intervals for each coordinate; to specify
the extents of the chunk it thus suffices to specify the endpoints
of the interval for each coordinate, or equivalently the coordinates
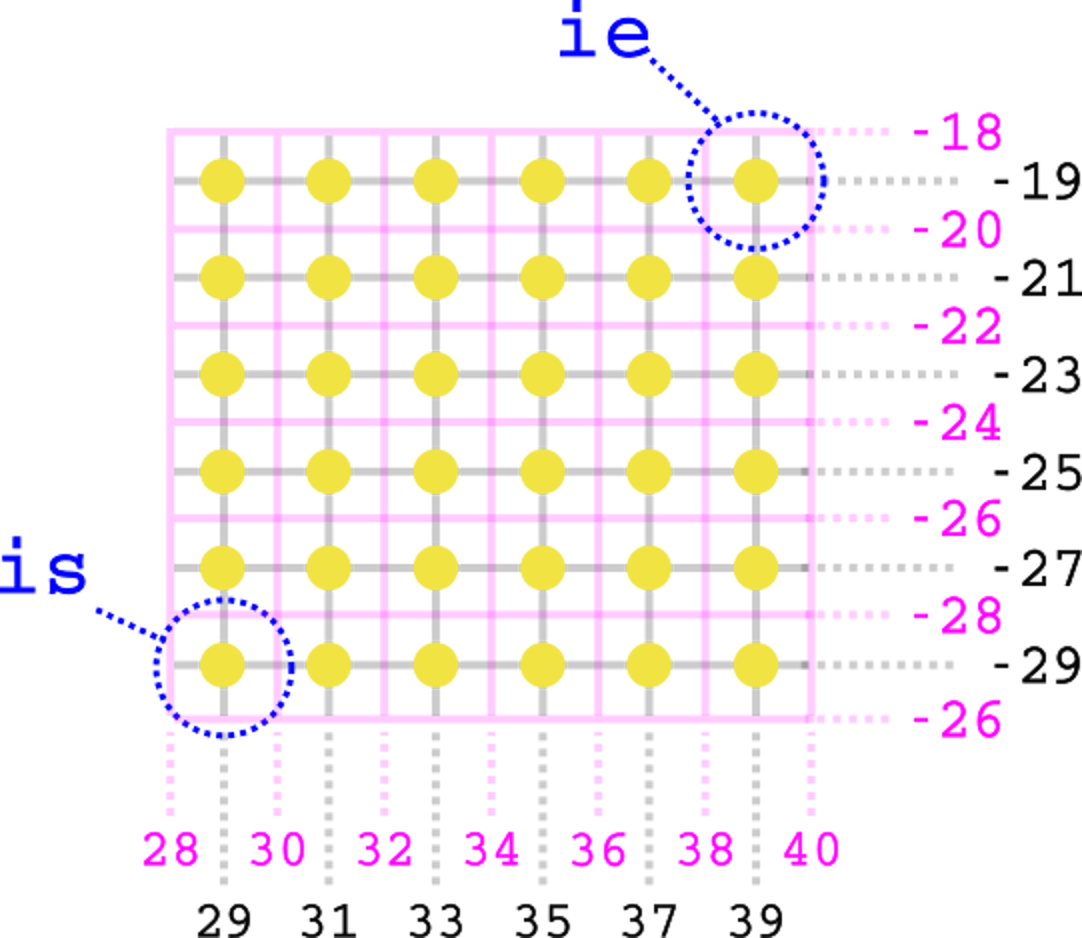
of the lower-left and upper-right grid points in the chunk. For each
chunk, these are represented by ivecs named is and ie
(stored in the fields_chunk and dft_chunk structures).
Here's an example of how this looks for chunk 3 in the figure above:
In this case we have is=(29,-29) and ie=(39,-19).
Chunking in the Multiprocessor Case#
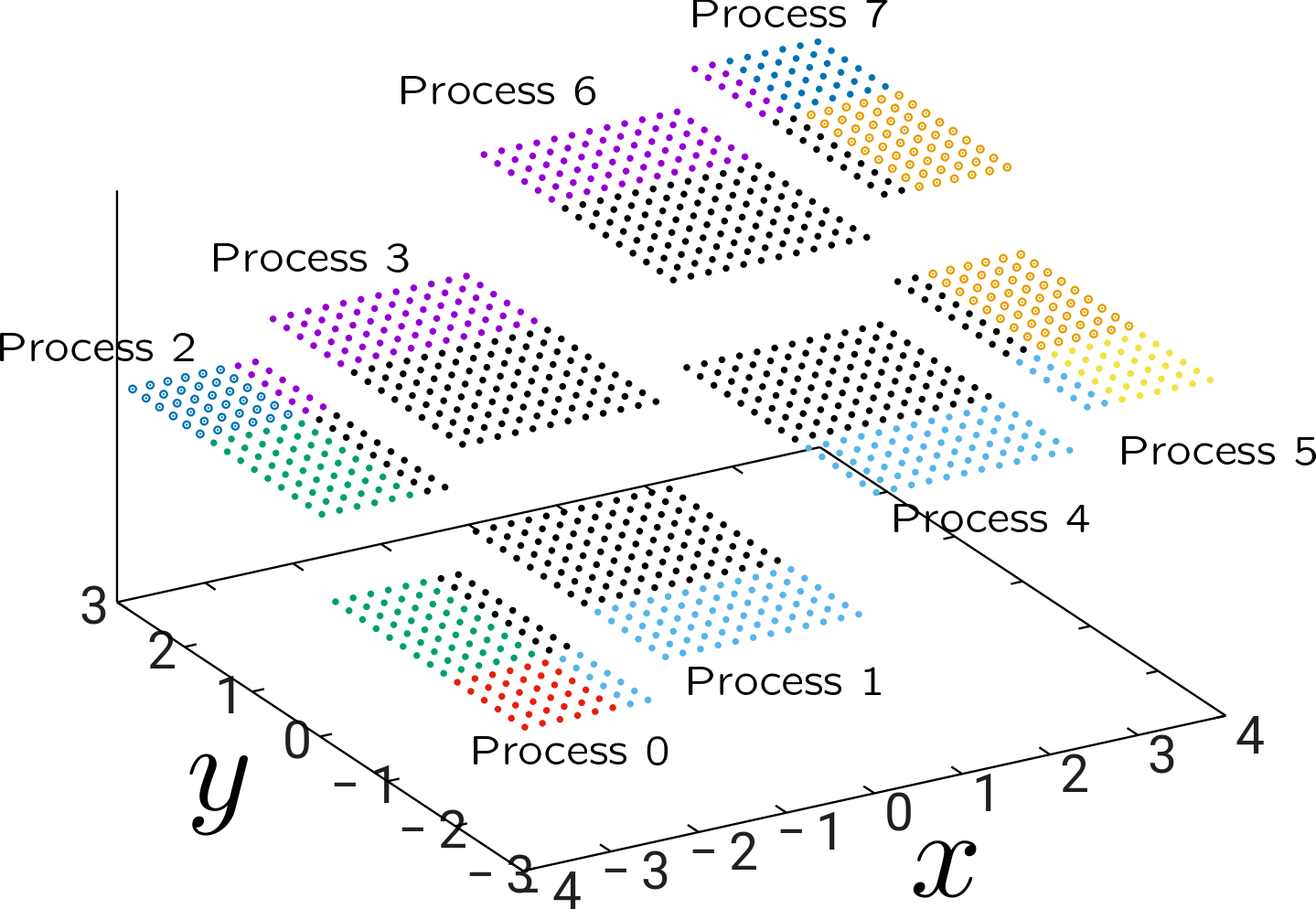
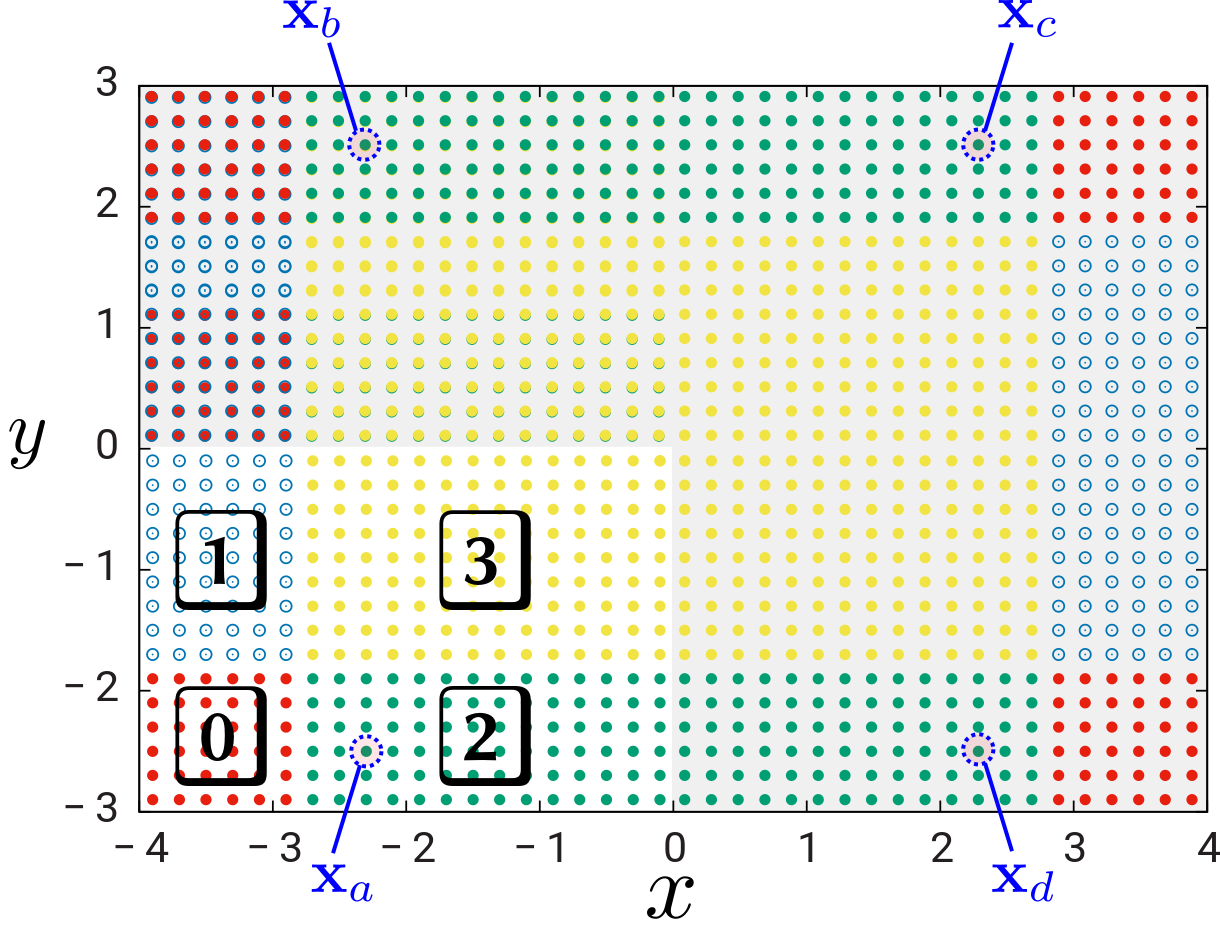
When running in parallel mode, each of the chunks identified for the single-processor case may be further subdivided into new chunks which can be assigned to different processors. For example, on a run with 8 processors, the 9 chunks identified in the single-processor case become 24 chunks:
In this image, grid points with different coordinates (different heights off the plane) are handled by different processors, while points with the same coordinate but different colors live in different chunks. In this case, processes 0, 2, 5, and 7 each own 4 chunks, while processes 1, 3, 4, and 6 each own 2 chunks.
Symmetries#
Meep's approach to handling symmetries is discussed from the user's perspective in Exploiting Symmetry and from a high-level algorithmic perspective in Computer Physics Communications, Vol. 181, pp. 687-702 (2010).
The following is a brief synopsis of the implementation of this feature.
-
The action of the symmetry group classifies grid points into orbits, sets of grid points that transform into one another under symmetry transformations. For example, in the figure with XY mirror symmetry below, the orbit of is . Meep chooses one element from each orbit (the "parent" grid point) to serve as a representative of the orbit, with the remaining elements of the orbit classified as "children" equivalent to the parent under the group action. (Any point in the orbit could serve equally well as the parent; the convention in meep is to choose the point with the lowest (most negative) grid indices, i.e the point closest to the lower-left corner of the overall grid--- in this case---but nothing depends on this particular choice.)
-
For each orbit, field components are only stored for the parent, not for any children. This reduces memory requirements by a factor , the number of points in each orbit, known in meep as the ``multiplicity'' of the symmetry; for example, for a geometry with Y-mirror symmetry, for an XY-mirror symmetry, for an N-fold rotational symmetry, etc.
-
Loops over grid points run only over parent points, i.e. points with field components stored in memory. However, each parent point is now visited times, once for each distinct symmetry transformation in the symmetry group (including the identity transformation). On the th visit to a given parent point , we
(1) look up the components of the fields stored in memory for ,
(2) apply the transformation to both the grid-point coordinates and the field components of the parent point to yield the coordinates and field components of the th child point, i.e. If the materials are anisotropic (i.e. the permittivity and/or permeability are tensors) we must transform those appropriately as well.
(3) use the coordinates and field components of the child point to carry out the operation in question.
Chunking in the Presence of Symmetries#
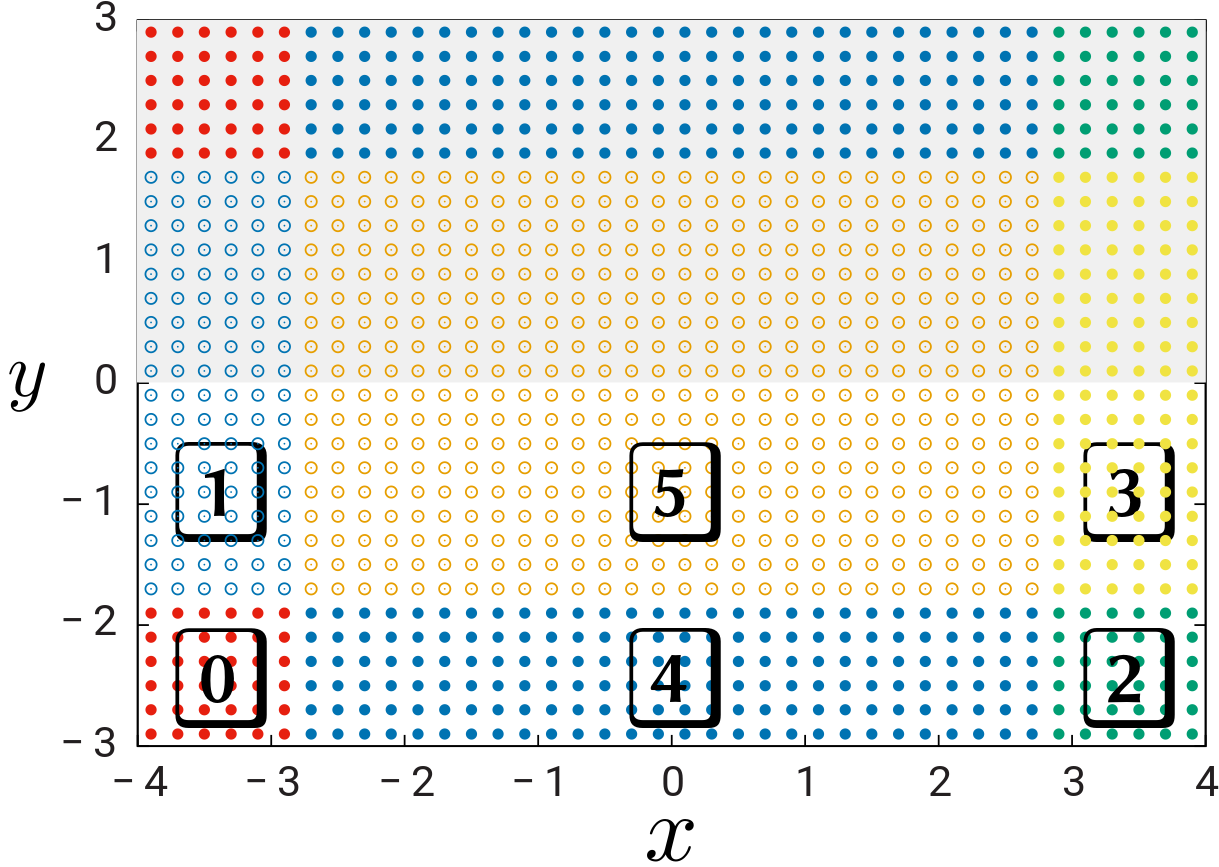
As noted above, in the presence of symmetries only a portion of the full grid is actually stored in memory. For example, adding a mirror symmetry (symmetry under reflection about the -axis) eliminates points in the upper half-plane ; the points that remain are now subdivided into 6 chunks (in the single-processor case):
Adding an mirror symmetry on top of this (so that now the geometry has both and mirror symmetry) reduces the number of stored grid points by an additional factor of 2; now the geometry is subdivided into just 4 chunks in the single-processor case:
In these figures, points in shaded regions are "children" — that is, points for which Meep stores no field components, since they are related by symmetry to "parent" points in the unshaded region. In the second figure we have indicated one complete orbit: parent point is carried to child points under the operations of the symmetry group.
Coordinates and Field Components of Symmetry-Reduced Points#
Symmetry transformations in libmeep are described by a class called
simply symmetry, which offers class methods for transforming grid
points and field components:
symmetry S = mirror(X,gv) + mirror(Y,gv); // XY mirror symmetry
ivec iparent; // grid indices of parent point
vec rparent; // cartesian coordinates of parent point
...
ivec ichild = S.transform(iparent, +1); // grid indices of child point
vec rchild = S.transform(rparent, +1); // cartesian coordinates of child point
component cchild = Ex; // desired field component at child point
component cparent = S.transform(cchild, -1); // corresponding component at parent point
The loop_in_chunks Routine#
To allow developers to implement loops over grid points without
stressing out over the various complications outlined above,
the fields class in libmeep offers a convenient method called
loop_in_chunks.
To use this routine, you will first write a "chunk-loop function"
which carries out some operation involving grid points and (optionally)
field components at grid points. Then you pass your routine to
loop_in_chunks with some additional arguments customizing the
type of loop you want (see below). Your loop function will then be
called once for every chunk in the problem---including both
chunks whose fields are present in memory, and those
whose aren't due to being eliminated by symmetry---with a long list
of arguments describing the chunk in question.
The body of your chunk-loop function will typically want to execute a loop over all grid points in the chunk. This is facilitated by a host of utility macros and API functions that operate on the arguments to your function to yield quantities of interest: grid-point coordinates, field-component values, etc.
The Chunk Loop Function#
The chunk-loop function that you write and pass to loop_in_chunks
has the following prototype:
void field_chunkloop(fields_chunk *fc, int ichunk, component cgrid, ivec is, ivec ie,
vec s0, vec s1, vec e0, vec e1, double dV0, double dV1,
ivec shift, std::complex<double> shift_phase,
const symmetry &S, int sn, void *chunkloop_data);
Notwithstanding this formidable-looking beast of a calling convention, most of the arguments here are things that you can blindly pass on to API functions and convenience macros, which will return quantities whose significance is easy to understand.
Here's a skeleton chunk-loop function
that executes a loop over all grid points in the chunk,
obtaining on each loop iteration both the integer indices and the cartesian
coordinates of the child point, as well as values for a list
of field components of interest (specified before the loop in the
constructor of chunkloop_field_components). You can fill in the rest of the loop body
to do whatever you want with ichild, rchild, and data.values, and the
results will be identical whether or not you declare symmetries when
defining your geometry. (Well, the results will be identical assuming
the physical problem you're considering really is symmetric, which Meep does not check.)
void my_chunkloop(fields_chunk *fc, int ichunk, component cgrid, ivec is, ivec ie,
vec s0, vec s1, vec e0, vec e1, double dV0, double dV1,
ivec shift, std::complex<double> shift_phase,
const symmetry &S, int sn, void *chunkloop_data)
{
// some preliminary setup
vec rshift(shift * (0.5*fc->gv.inva)); // shift into unit cell for PBC geometries
// prepare the list of field components to fetch at each grid point
component components[] = {Ex, Hz};
chunkloop_field_components data(fc, cgrid, shift_phase, S, sn, 2, components);
// loop over all grid points in chunk
LOOP_OVER_IVECS(fc->gv, is, ie, idx)
{
// get grid indices and coordinates of parent point
IVEC_LOOP_ILOC(gv, iparent); // grid indices
IVEC_LOOP_LOC(gv, rparent); // cartesian coordinates
// apply symmetry transform to get grid indices and coordinates of child point
ivec ichild = S.transform(iparent, sn) + shift;
vec rchild = S.transform(rparent, sn) + rshift;
// fetch field components at child point
data.update_values(idx);
std::complex<double> Ex = data.values[0],
Hz = data.values[1];
}
}
Is There a Version of loop_in_chunks for dft_chunks?#
No, but the routine process_dft_component() in src/dft.cpp effectively
implements such a routine for a hard-coded set of operations on DFT
components (namely: outputting to HDF5, fetching DFT array slices,
and computing mode-overlap coefficients).
How the Images were Created#
The images above were obtained with the help of a simple C++ code
called WriteChunkInfo that calls libmeep API functions to
obtain info on the chunk structure of the 40×30 grid
we considered. This code (plus a simple hand-written Makefile)
lives in the doc/docs/Developer_Codes subdirectory of the meep source
distribution.